Class 6 - Mathematics
Chapter - Congruence of Triangles : Exercise 7.2

Top Block 1
Question: 1.Which congruence criterion do you use in the following?
(a) Given: AC = DF, AB = DE, BC = EF
(b) Given: RP = ZX, RQ = ZY, ∠PRQ = ∠XZY
Mddle block 1
(c) Given: ∠MLN = ∠FGH, ∠NML = ∠HFG, ML = FG

(d) Given: EB = BD, AE = CB, ∠A = ∠C = 90o

Answer :
(a) By SSS congruence criterion, since it is given that AC = DF, AB = DE, BC = EF
The three sides of one triangle are equal to the three corresponding sides of another triangle.
Therefore, ΔABC ≅ ΔDEF
(b) By SAS congruence criterion, since it is given that RP = ZX, RQ = ZY and ∠PRQ = ∠XZY
The two sides and one angle in one of the triangle are equal to the corresponding sides and the angle of other triangle.
Therefore, ΔPQR ≅ ΔXYZ
(c) By ASA congruence criterion, since it is given that ∠MLN = ∠FGH, ∠NML = ∠HFG, ML = FG.
The two angles and one side in one of the triangle are equal to the corresponding angles and side of other triangle.
Therefore, ΔLMN ≅ ΔGFH
(d) By RHS congruence criterion, since it is given that EB = BD, AE = CB, ∠A = ∠C = 90o
Hypotenuse and one side of a right angled triangle are respectively equal to the hypotenuse and one side of another right angled triangle.
Therefore, ΔABE ≅ ΔCDB
Question: 2.You want to show that ΔART ≅ ΔPEN:
If you have to use SSS criterion, then you need to show:
(i) AR = (ii) RT = (iii) AT =
If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have:
(i) RT = and(ii) PN =
If it is given that AT = PN and you are to use ASA criterion, you need to have:
(i) ? (ii) ?

Answer :
(a) Using SSS criterion, ΔART ≅ ΔPEN
(i) AR = PE (ii) RT = EN (iii) AT = PN
(b) Given: ∠T = ∠N
Using SAS criterion, ΔART ≅ ΔPEN
(i) RT = EN (ii) PN = AT
(c) Given: AT = PN
Using ASA criterion, ΔART ≅ ΔPEN
(i) ∠RAT = ∠EPN (ii) ∠RTA = ∠ENP
Question: 3.You have to show that ΔAMP ≅ ΔAMQ. In the following proof, supply the missing reasons:

| Steps | Reasons |
|---|---|
| PM = QM | __________ |
| ∠PMA = ∠QMA | __________ |
| AM = AM | __________ |
| ΔAMP ≅ ΔAMQ | __________ |
Answer :
| Steps | Reasons |
|---|---|
| PM = QM | Given |
| ∠PMA = ∠QMA | Given |
| AM = AM | Common |
| ΔAMP ≅ ΔAMQ | SAS congruence rule |
Question: 4.In ΔABC, ∠A = 30o, ∠B = 40o and ∠C = 110o.
In ΔPQR, ∠P = 30o, ∠Q = 40o and ∠R = 110o.
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified? Why or why not?
Answer :
No, because the two triangles with equal corresponding angles need not be congruent. In such a correspondence, one of them can be an enlarged copy of the other.
Question: 5.In the figure, the two triangles are congruent. The corresponding parts are marked. We can write ΔRAT ≅ ?

Answer :
In the figure, given two triangles are congruent. So, the corresponding parts are:
A ↔ O, R ↔ W, T ↔ N.
We can write, ΔRAT ≅ ΔWON [By SAS congruence rule]
Question: 6.Complete the congruence statement:
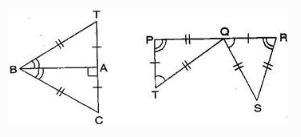
Answer :
In ΔBAT and ΔBAC, given triangles are congruent so the corresponding parts are:
B ↔ B, A ↔ A, T ↔ C
Thus, ΔBCA ≅ ΔBTA [By SSS congruence rule]
In ΔQRS and ΔTPQ, given triangles are congruent so the corresponding parts are:
P ↔ R, T ↔ Q, Q ↔ S
Thus, ΔQRS ≅ ΔTPQ [By SSS congruence rule]
Question: 7.In a squared sheet, draw two triangles of equal area such that:
(i) the triangles are congruent.
(ii) the triangles are not congruent.
What can you say about their perimeters?
Answer :
In a squared sheet, draw ΔABC and ΔPQR.
When two triangles have equal areas and
(i) these triangles are congruent, i.e., ΔABC ≅ ΔPQR
[By SSS congruence rule]
Then, their perimeters are same because length of sides of first triangle are equal to the length of sides of another triangle by SSS congruence rule.
(ii) But, if the triangles are not congruent, then their perimeters are not same because lengths of sides of first triangle are not equal to the length of corresponding sides of another triangle.
Question: 8.Draw a rough sketch of two triangles such that they have five pairs of congruent parts but still the triangles are not congruent.
Answer :
Let us draw two triangles PQR and ABC.
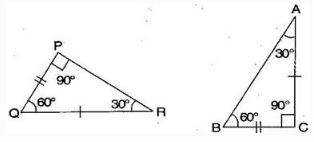
Question: 9.If ΔABC and ΔPQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?

Answer :
ΔABC and ΔPQR are congruent. Then one additional pair is BC = QR.
Given: ∠B = ∠Q = 90o
∠C = ∠R
BC = QR
Therefore, ΔABC ≅ ΔPQR [By ASA congruence rule]
Question: 10.Explain, why ΔABC ≅ ΔFED.
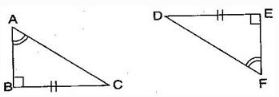
Answer :
Given: ∠A = ∠F, BC = ED, ∠B = ∠E
In ΔABC and ΔFED,
∠B = ∠E = 90o
∠A = ∠F
BC = ED
Therefore, ΔABC ≅ ΔFED [By RHS congruence rule]

