Class 6 - Mathematics
Chapter - Triangles and its Properties : Exercise 6.4

Top Block 1
Question: 1.Is it possible to have a triangle with the following sides?
2 cm, 3 cm, 5 cm
3 cm, 6 cm, 7 cm
6 cm, 3 cm, 2 cm
Answer :
Since, a triangle is possible whose sum of the lengths of any two sides would be greater than the length of third side.
(i) 2 cm, 3 cm, 5 cm
2 + 3 > 5 No
2 + 5 > 3 Yes
3 + 5 > 2 Yes
This triangle is not possible.
(ii) 3 cm, 6 cm, 7 cm
3 + 6 > 7 Yes
6 + 7 > 3 Yes
3 + 7 > 6 Yes
This triangle is possible.
(iii) 6 cm, 3 cm, 2 cm
6 + 3 > 2 Yes
6 + 2 > 3 Yes
2 + 3 > 6 No
This triangle is not possible.
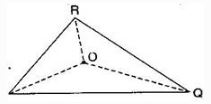
Question: 2.Take any point O in the interior of a triangle PQR. Is:

OQ + OR >QR ?
OR + OP >RP ?
Since sum of two sides is greater than third side.
Answer :
Join OR, OQ and OP.
Mddle block 1
Yes, POQ form a triangle.
(ii) Is OQ + OR > QR ?
Yes, RQO form a triangle.
(iii) Is OR + OP > RP ?
Yes, ROP form a triangle.
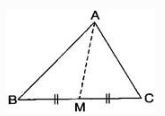
Question: 3.AM is a median of a triangle ABC. Is AB + BC + CA > 2AM ?
Answer :
Since, the sum of lengths of any two sides in a triangle should be greater than the length of third side.
Therefore, In ΔABM, AB + BM > AM ……….(i)
In ΔAMC, AC + MC > AM ……….(ii)
Adding eq. (i) and (ii),
AB + BM + AC + MC > AM + AM
⇒ AB + AC + (BM + MC) > 2AM
⇒ AB + AC + BC > 2AM
Hence, it is true.
Question: 4.ABCD is a quadrilateral. Is AB + BC + CD + DA > AC + BD ?

Answer :
Since, the sum of lengths of any two sides in a triangle should be greater than the length of third side.
Therefore, In ΔABC, AB + BC > AC ……….(i)
In ΔADC, AD + DC > AC ……….(ii)
In ΔDCB, DC + CB > DB ……….(iii)
In ΔADB, AD + AB > DB ……….(iv)
Adding eq. (i), (ii), (iii) and (iv),
AB + BC + AD + DC + DC + CB + AD + AB > AC + AC + DB + DB
⇒ (AB + AB) + (BC + BC) + (AD + AD) + (DC + DC) > 2AC + 2DB
⇒ 2AB + 2BC + 2AD + 2DC > 2(AC + DB)
⇒ 2(AB + BC + AD + DC) > 2(AC + DB)
⇒ AB + BC + AD + DC > AC + DB
⇒ AB + BC + CD + DA > AC + DB
Hence, it is true.
Question: 5. ABCD is quadrilateral. Is AB + BC + CD + DA < 2 (AC + BD) ?
Answer :
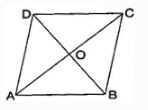
Therefore, In ΔAOB, AB < OA + OB ……….(i)
In ΔBOC, BC < OB + OC ……….(ii)
In ΔCOD, CD < OC + OD ……….(iii)
In ΔAOD, DA < OD + OA ……….(iv)
Adding eq. (i), (ii), (iii) and (iv),
AB + BC + CD + DA < OA + OB + OB + OC + OC + OD + OD + OA
⇒ AB + BC + CD + DA < 2OA + 2OB + 2OC + 2OD
⇒ AB + BC + CD + DA < 2[(AO + OC) + (DO + OB)]
⇒ AB + BC + CD + DA < 2(AC + BD)
Hence, it is proved.
Question: 6.The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
Answer :
Since, the sum of lengths of any two sides in a triangle should be greater than the length of third side.
It is given that two sides of triangle are 12 cm and 15 cm.
Therefore, the third side should be less than 12 + 15 = 27 cm.
And also the third side cannot be less than the difference of the two sides.
Therefore, the third side has to be more than 15 – 12 = 3 cm.
Therefore, the third side could be the length more than 3 cm and less than 27 cm.

