Class 8 - Mathematics
Understanding Quadrilaterals - Exercise 3.1

Top Block 1
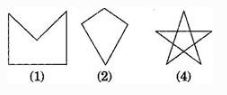
Question: 1. Given here are some figures:
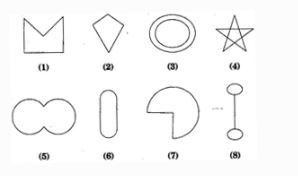
(a) Simple curve
(b) Simple closed curve
(c) Polygon
(d) Convex polygon
(e) Concave polygon
Answer :
(a) Simple curve
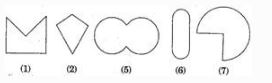

Mddle block 1

Question: 2. How many diagonals does each of the following have?
(a) A convex quadrilateral
(b) A regular hexagon
(c) A triangle
Answer :
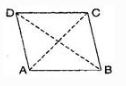
(a) A convex quadrilateral has two diagonals.
Here, AC and BD are two diagonals.
Here, diagonals are AD, AE, BD, BE, FC, FB, AC, EC and FD.

Question: 3. What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try)
Answer :
Let ABCD is a convex quadrilateral, then we draw a diagonal AC which divides the quadrilateral in two triangles.
∠A + ∠B + ∠C + ∠D
= ∠1 + ∠6 + ∠5 + ∠4 + ∠3 + ∠2
= (∠1 + ∠2 + ∠3) + (∠4 + ∠5 + ∠6)
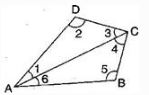
[By Angle sum property of triangle]
= 360°
Hence, the sum of measures of the triangles of a convex quadrilateral is 360°
Yes, if quadrilateral is not convex then, this property will also be applied.
Let ABCD is a non-convex quadrilateral and join BD, which also divides the quadrilateral in two triangles.
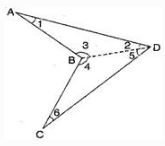
In ΔABD, ∠1 + ∠2 + ∠3 = 180° ……….(i)
In ΔBDC, ∠4 + ∠5 + ∠6 = 180° ……….(ii)
Adding eq. (i) and (ii),
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 = 360°
∠1 + ∠2 + (∠3 + ∠4) + ∠5 + ∠6
= 360°
∠A + ∠B + ∠C + ∠D = 360°
Hence proved.
Question: 4. Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.) What can you say about the angle sum of a convex polygon with number of sides?
Answer :
(a) When n = 7, then
Angle sum of a polygon = (n – 2) x 180°
=(7 – 2) x 180° = 5 x 180° = 900°
(b) When n = 8, then
Angle sum of a polygon = (n – 2) x 180°
= (8 – 2) x 180°
= 6 x 180° = 1080°
(c) When n = 10, then
Angle sum of a polygon = (n – 2) x 180°
(10 – 2) x 180°
= 6 x 180° = 1440°
(d) When n = n then
Angle sum of a polygon = (n – 2) x 180°
Question: 5. What is a regular polygon? State the name of a regular polygon of:
(a) 3 sides
(b) 4 sides
(c) 6 sides
Answer :
A regular polygon: A polygon having all sides of equal length and the interior angles of equal size is known as regular polygon.
(i) 3 sides
Polygon having three sides is called a triangle.
(ii) 4 sides
Polygon having four sides is called a quadrilateral.
(iii) 6 sides
Polygon having six sides is called a hexagon.
Question: 6. Find the angle measures in the following figures:

Answer :
(a) Using angle sum property of a quadrilateral,

⇒ 300° + 𝓍 = 360°
⇒ 𝓍 = 360° – 300°
⇒ 𝓍 = 60°
(b) Using angle sum property of a quadrilateral,
⇒ 220° + 𝓍 = 360°
⇒ 𝓍 = 360° – 220°
⇒ 𝓍 = 140°
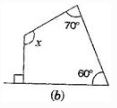
(c) First base interior angle
= 180° – 70° = 110°
Second base interior angle
= 180° – 60° = 120°
There are 5 sides, n = 5

= (5 – 2) x 180° = 3 x 180° = 540°
∴ 30° + 𝓍 + 110° + 𝓍 = 540°
⇒ 260° + 2𝓍 = 540°
⇒ 2𝓍 = 540° – 260°
⇒ 2𝓍 = 280°
⇒ 𝓍 = 140°
(d) Angle sum of a polygon = (n – 2) x 180°
= (5 – 2) x 180° = 3 x 180° = 540°
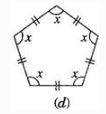
⇒ 5∠𝓍 = 540°
⇒ ∠𝓍 = 108°
Hence each interior angle is 108°
Question: 7. (a) Find


Answer :
(a) Since sum of linear pair angles is

⇒ 𝓍 = 180° – 90°
⇒ 𝓍 = 90°
And
z = 180° – 30°
z = 150°
Also y = 90° + 30° = 120°
[Exterior angle property]
∴ 𝓍 + 𝓎 + 𝓏 = 90° + 120° + 180° = 360°
(b) Using angle sum property of a quadrilateral,

⇒ 260° + n = 360°
⇒ n = 360° – 260°
⇒ n = 100°
Since sum of linear pair angles is 180°
∴ w + 100° = 180° ……….(i)
x + 120° = 180° ……….(ii)
y + 80° = 180° ……….(iii)
z + 60° = 180° ……….(iv)
Adding eq. (i), (ii), (iii) and (iv),
w + 100° + x + 120° + y + 80° + z + 60° = 720°
w + x + y + z + 100° + 120° + 80° + 60° = 720°
w + x + y + z + 360° = 720°
w + x + y + z = 720° – 360°
w + x + y + z = 360°

