Class 9 - Mathematics
Areas of Parallelograms and Triangles - Exercise 9.2

Top Block 1
Exercise 9.2
Question : 1 : In the figure, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
Answer :
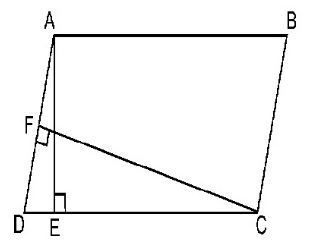
Area of parallelogram ABCD = AB * AE
= 16 * 8
= 128 cm2
Also, area of parallelogram ABCD = AD * FC
⇒ AD * 10 = 128
⇒ AD = 128/10
⇒ AD = 12.8 cm
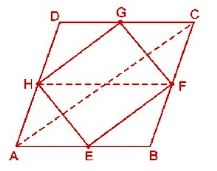
Question : 2: If E, F, G, and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH) = ar(ABCD)/2.
Answer :
Mddle block 1
Given: A parallelogram ABCD • E, F, G, H are mid-points of sides AB, BC, CD, DA respectively.
To Prove: ar(EFGH) = ar(ABCD)/2
Construction : Join AC and HF.
Proof : In ∆ABC,
E is the mid-point of AB. F is the mid-point of BC.
⇒ EF is parallel to AC and EF = AC/2 ………..1
Similarly, in ∆ADC, we can show that
HG || AC and HG = AC/2 ………..2
From equation 1 and 2, we get
EF || HG and EF = HG
So, EFGH is a parallelogram. [One pour of opposite sides is equal and parallel]
In quadrilateral ABFH, we have
HA = FB and HA || FB [AD = BC ⇒ AD/2 = BC/2 ⇒ HA = FB]
So, ABFH is a parallelogram. [One pair of opposite sides is equal and parallel]
Now, triangle HEF and parallelogram HABF are on the same base HF and between the same
parallels HF and AB.
Now, Area of ∆HEF = area of HABF/2 ………..3
Similarly, area of ∆HGF = area of HFCD/2 ………4
Adding equation 3 and 4, we get
Area of ∆HEF + area of ∆HGF = (area of HABF + area of HFCD)/2
⇒ ar(EFGH) = ar(ABCD)
Hence, Proved.
Question : 3: P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB) = ar(BQC).
Answer :

Given: A parallelogram ABCD. P and Q are any points on DC and AD respectively.
To prove: ar(APB) = ar(BQC)
Construction: Draw PS || AD and QR || AB.
Proof: In parallelogram ABRQ, BQ is the diagonal.
So, area of ∆BQR = area of ABRQ/2 ………….1
In parallelogram CDQR, CQ is a diagonal.
So, area of ∆RQC = area of CDQR/2 …………2
Adding equation 1 and 2, we get
area of ∆BQR + area of ∆RQC = (area of ABRQ + area of CDQR)/2
⇒ area of ∆BQC = area of ABCD/2 ………3
Again, in parallelogram DPSA, AP is a diagonal.
So, area of ∆ASP = area of DPSA/2 ……….4
In parallelogram BCPS, PB is a diagonal.
Now, area of ∆BPS = area of BCPS/2 ……….5
Adding equation 4 and 5, we get
area of ∆ASP + area of ∆BPS = (area of DPSA + area of BCPS)/2
⇒ area of ∆APB = (area of ABCD) ……..6
From equation 3 and 6, we have
area of ∆APB = area of ∆BQC.
Hence, Proved.
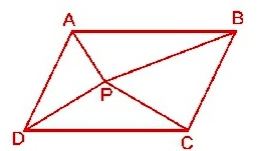
Question : 4: In the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(APB) + ar(PCD) = ar(ABCD)/2
(ii) ar(APD) + ar(PBC) = ar(APB) + ar(PCD)
Answer :
Given: A parallelogram ABCD. P is a point inside it.
To prove:
(i) ar(APB) + ar(PCD) = ar(ABCD)/2
(ii) ar(APD) + ar(PBC) = ar(APB) + ar(PCD)
Construction: Draw EF through P parallel to AB, and GH through P parallel to AD.

Proof: In parallelogram FPGA, AP is a diagonal,
So, area of ∆APG = area of ∆APF …………..1
In parallelogram BGPE, PB is a diagonal,
So, area of ∆BPG = area of ∆EPB …………..2
In parallelogram DHPF, DP is a diagonal,
area of ∆DPH = area of ∆DPF ……….3
In parallelogram HCEP, CP is a diagonal,
So, area of ∆CPH = area of ∆CPE …..4
Adding equation 1, 2, 3 and 4, we get
area of ∆APG + area of ∆BPG + area of ∆DPH + area of ∆CPH
= area of ∆APF + area of ∆EPB + area of ∆DPF + area ∆CPE
⇒ [area of ∆APG + area of ∆BPG] + [area of ∆DPH + area of ∆CPH]
= [area of ∆APF + area of ∆DPF] + [area of ∆EPB + area of ∆CPE]
⇒ area of ∆APB + area of ∆CPD = area of ∆APD + area of ∆BPC ……..5
But area of parallelogram ABCD
= area of ∆APB + area of ∆CPD + area of ∆APD + area of ∆BPC ……….6
From equation 5 and 6, we get
area of ∆APB + area of ∆PCD = area of ABCD/2
⇒ ar(APB) + ar(PCD) = ar(ABCD)/2
Hence, Proved.
From equation 5,
⇒ ar (APD) + ar (PBC) = ar (APB) + ar (CPD)
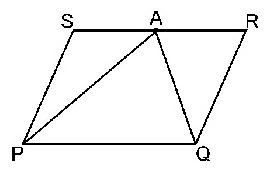
Question : 5: In the figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar(PQRS) = ar(ABRS)
(ii) ar(AXS) = ar(PQRS)/2

Answer :
Given: PQRS and ABRS are parallelograms and X is any point on side BR.
To prove:
(i) ar(PQRS) = ar(ABRS)
(ii) ar(AXS) = ar(PQRS)/2
(i) In ∆ASP and BRQ, we have,
∠SPA = ∠RQB [Corresponding angles] …(1)
∠PAS = ∠QBR [Corresponding angles] …(2)
So, ∠PSA = ∠QRB [Angle sum property of a triangle] …(3)
Also, PS = QR [Opposite sides of the parallelogram PQRS] …(4)
So, ∆ASP ≅∆BRQ [ASA axiom, using (1), (3) and (4)]
Therefore, area of ∆PSA = area of ∆QRB [Congruent figures have equal areas] …(5)
Now, ar(PQRS) = ar(PSA) + ar(ASRQ)
= ar(QRB) + ar(ASRQ)
= ar(ABRS)
So, ar(PQRS) = ar(ABRS) Proved.
(ii) Now, ∆AXS and ||gm ABRS are on the same base AS and between same parallels AS and BR
So, area of ∆AXS = area of ABRS/2
⇒ area of ∆AXS = area of PQRS/2 [Since ar(PQRS) = ar(ABRS]
⇒ ar of (AXS) = ar of (PQRS)/2
Question : 6: A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q.
In how many parts the fields is divided? What are the shapes of these parts?
The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?
Answer :
The field is divided in three triangles.
Since triangle APQ and parallelogram PQRS are on the same base PQ and between the same
parallels PQ and RS.
So, ar(APQ) = ar(PQRS)/2
⇒ 2ar(APQ) = ar(PQRS)
But ar(PQRS) = ar(APQ) + ar(PSA) + ar(ARQ)
⇒ 2 ar(APQ) = ar(APQ) + ar(PSA) + ar(ARQ)
⇒ ar(APQ) = ar(PSA) + ar(ARQ)
Hence, area of ∆APQ = area of ∆PSA + area of ∆ARQ.
To sow wheat and pulses in equal portions of the field separately, farmer sow wheat in ∆APQ
and pulses in other two triangles or pulses in ∆APQ and wheat in other two triangles.

