Class 9 - Mathematics
Circles - Exercise 10.5

Top Block 1
Exercise 10.5
Question :1 : In Fig. 10.36, A,B and C are three points on a circle with centre O such that ∠ BOC = 300 and ∠ AOB = 60°.
If D is a point on the circle other than the arc ABC, find ∠ADC.
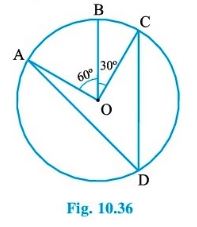
Answer :
We have, ∠BOC = 300 and ∠AOB = 600
Now, ∠AOC = ∠AOB + ∠BOC
= 600 + 300
= 900
We know that angle subtended by an arc at the centre of a circle is double the angle
subtended by the same arc on the remaining part of the circle.
So, 2∠ADC = ∠AOC
⇒ ∠ADC = ∠AOC/2
= 900/2
⇒ ∠ADC = 450
Question : 2 : A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Answer :

Mddle block 1
We have, OA = OB = AB
Therefore, ∆OAB is a equilateral triangle.
⇒ ∠AOB = 600
We know that angle subtended by an arc at the centre of a circle is double the angle
subtended by the same arc on the remaining part of the circle.
So, ∠AOB = 2∠ACB
⇒ ∠ACB = ∠AOB/2
= 600/2
⇒ ∠ACB = 300
Also, ∠ADB = reflex ∠AOB/2
= (3600 – 600)/2
= 3000/2
= 1500
Question : 3: In Fig. 10.37, ∠ PQR = 1000, where P, Q and R are points on a circle with centre O. Find ∠ OPR

Answer :
Reflex angle POR = 2∠PQR
= 2 * 1000
= 2000
Now, angle POR = 3600 – 2000 = 1600
Also, PO = OR [Radii of a circle]
∠OPR = ∠ORP [Opposite angles of isosceles triangle]
In ∆OPR,
∠POR = 1600
So, ∠OPR = ∠ORP = 100 [Angle sum property of a triangle]
Question : 4: In Fig. 10.38, ∠ ABC = 690, ∠ ACB = 310, find ∠ BDC.

Answer :
In Δ ABC, we have
∠ ABC + ∠ ACB + ∠ BAC = 1800 [Angle sum property of a triangle]
⇒ 690 + 310 + ∠ BAC = 1800
⇒ 1000 + ∠ BAC = 1800
⇒ ∠ BAC = 1800– 1000
⇒ ∠ BAC = 800
Also, ∠ BAC = ∠ BDC [Angles in the same segment]
So, ∠ BDC = 800
Question : 5: In Fig. 10.39, A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠ BEC = 1300 and ∠ ECD = 200. Find ∠ BAC

Answer :
From the figure,
∠ BEC + ∠ DEC = 1800 [Linear pair]
⇒ 1300 + ∠ DEC = 1800
⇒ ∠ DEC = 1800 – 1300
⇒ ∠ DEC = 500
Now, in Δ DEC,
∠ DEC + ∠ DCE + ∠ CDE = 1800 [Angle sum property of a triangle]
⇒ 500 + 200 + ∠ CDE = 1800
⇒ 700 + ∠ CDE = 1800
⇒ ∠ CDE = 1800– 700
⇒ ∠ CDE = 1100
Also, ∠ CDE = ∠ BAC [Angles in same segment]
⇒ ∠ BAC = 1100
Question : 6: ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠ DBC = 700, ∠ BAC is 300, find ∠ BCD. Further, if AB = BC, find ∠ ECD.
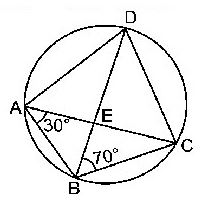
Answer :
From the figure,
∠CAD = ∠DBC= 700 [Angles in the same segment]
Therefore, ∠DAB = ∠CAD + ∠BAC
= 700 + 300
= 1000
But, ∠DAB + ∠BCD = 1800 [Opposite angles of a cyclic quadrilateral]
So, ∠BCD = 1800– 1000
= 800
Now, we have AB = BC
Therefore, ∠BCA = 300 [Opposite angles of an isosceles triangle]
Again, ∠DAB + ∠BCD = 1800 [Opposite angles of a cyclic quadrilateral]
⇒ 1000 + ∠BCA + ∠ECD = 1800 [Since ∠BCD = ∠BCA + ∠ECD]
⇒ 1000 + 300 + ∠ECD = 1800
⇒ 1300 + ∠ECD = 1800
⇒ ∠ECD = 1800– 1300
⇒ ∠ECD = 500
Hence, ∠BCD = 800 and ∠ECD = 500
Question : 7: If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
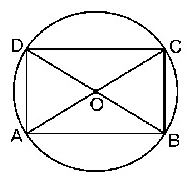
Answer :
Given: ABCD is a cyclic quadrilateral, whose diagonals AC and BD are diameter of the circle
Passing through A, B, C and D.
To Prove: ABCD is a rectangle.
Proof:
In ∆AOD and ∆COB,
AO = CO [Radii of a circle]
OD = OB [Radii of a circle]
∠AOD = ∠COB [Vertically opposite angles]
So, ∆AOD ≅∆COB [by SAS axiom]
Hence, ∠OAD = ∠OCB [by CPCT]
But these are alternate interior angles made by the transversal AC, intersecting AD and BC.
So, AD || BC
Similarly, AB || CD.
Hence, quadrilateral ABCD is a parallelogram.
Also, ∠ABC = ∠ADC ………….(i) [Opposite angles of a parallelogram are equal]
And, ∠ABC + ∠ADC = 1800 …(ii) [Sum of opposite angles of a cyclic quadrilateral is 1800]
⇒ ∠ABC = ∠ADC = 900 [From equation (i) and (ii)]
So, ABCD is a rectangle. [A parallelogram one of whose angles is 900 is a rectangle]
Question : 8: If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
Answer :
Given: A trapezium ABCD in which AB || CD and AD = BC.
To Prove: ABCD is a cyclic trapezium.
Construction: Draw DE ⊥ AB and CF ⊥ AB.

Proof:
In ∆DEA and ∆CFB, we have
AD = BC [Given]
∠DEA = ∠CFB = 900 [DE ⊥ AB and CF ⊥ AB]
DE = CF [Distance between parallel lines remains constant]
So, ∆DEA ≅∆CFB [by RHS axiom]
⇒ ∠A = ∠B ………(i) [by CPCT]
and, ∠ADE = ∠BCF ……..(ii) [by CPCT]
Since, ∠ADE = ∠BCF [From equation (ii)]
⇒ ∠ADE + 900 = ∠BCF + 900 ⇒ ∠ADE + ∠CDE = ∠BCF + ∠DCF
⇒ ∠D = ∠C ………..(iii) [∠ADE + ∠CDE = ∠D, ∠BCF + ∠DCF = ∠C]
So, ∠A = ∠B and ∠C = ∠D ……(iv) [From (i) and (iii)]
⇒ ∠A + ∠B + ∠C + ∠D = 3600 [Sum of the angles of a quadrilateral is 360°]
⇒ 2(∠B + ∠D) = 3600 [Using equation (iv)]
⇒ ∠B + ∠D = 1800
⇒ Sum of a pair of opposite angles of quadrilateral ABCD is 1800.
⇒ ABCD is a cyclic trapezium
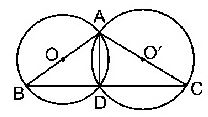
Question : 9: Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig. 10.40). Prove that ∠ ACP = ∠ QCD

Answer :
Given: Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ
are drawn to intersect the circles at A, D and P, Q respectively.
To Prove: ∠ACP = ∠QCD.
Proof:
∠ACP = ∠ABP ……….(i) [Angles in the same segment]
∠QCD = ∠QBD ………(ii) [Angles in the same segment]
But, ∠ABP = ∠QBD ..(iii) [Vertically opposite angles]
From equation (i), (ii) and (ii), we get
∠ACP = ∠QCD
Question : 10: If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
Answer :
Given: Sides AB and AC of a triangle ABC are diameters of two circles which intersect at D.
To Prove: D lies on BC.
Proof: Join AD
∠ADB = 900 ……….(i) [Angle in a semicircle]
Also, ∠ADC = 900………..(ii)
Adding equation (i) and (ii), we get
∠ADB + ∠ADC = 900 + 900
⇒ ∠ADB + ∠ADC = 1800
⇒ BDC is a straight line.
So, D lies on BC
Hence, point of intersection of circles lie on the third side BC.
Question : 11: ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Answer :

Given: ABC and ADC are two right triangles with common hypotenuse AC.
To Prove: ∠CAD = ∠CBD
Proof: Let O be the mid-point of AC.
Then OA = OB = OC = OD
Mid point of the hypotenuse of a right triangle is equidistant from its vertices with O as centre
and radius equal to OA, draw a circle to pass through A, B, C and D.
We know that angles in the same segment of a circle are equal.
Since, ∠CAD and ∠CBD are angles of the same segment.
Therefore, ∠CAD = ∠CBD.
Question : 12: Prove that a cyclic parallelogram is a rectangle.
Answer :
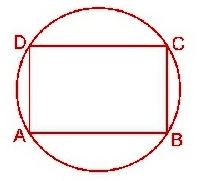
Given: ABCD is a cyclic parallelogram.
To prove: ABCD is a rectangle.
Proof: ∠ABC = ∠ADC …………(i) [Opposite angles of a parallelogram are equal]
But, ∠ABC + ∠ADC = 1800 … (ii) [Sum of opposite angles of a cyclic quadrilateral is 1800]
⇒∠ABC = ∠ADC = 900 [From equation (i) and (ii)]
So, ABCD is a rectangle [A parallelogram one of whose angles is 900 is a rectangle]
Hence, a cyclic parallelogram is a rectangle.

