Class 9 - Mathematics
Constructions - Exercise 11.1

Top Block 1
Question : 1 : Construct an angle of 900 at the initial point of a given ray and justify the construction.
Answer :
Steps of Construction:

(i) Let us take a ray AB with initial point A.
(ii) Taking A as centre and some radius, draw an arc of a circle, which intersects AB at C.
(iii) With C as centre and the same radius as before, draw an arc, intersecting the previous arc
at E.
(iv) With E as centre and the same radius, as before, draw an arc, which intersects the arc
drawn in step (ii) at F.
(v) With E as centre and some radius, draw an arc.
(vi) With F as centre and the same radius as before, draw another arc, intersecting the
previous arc at G.
(vii) Draw the ray AG.
Then BAG is the required angle of 900.
Justification: Join AE, CE, EF, FG and GE
AC = CE = AE [By construction]
ΔACE is an equilateral triangle
Angle CAE = 60° .……..………(i)
Similarly, ΔAEF = 60° ………… (ii)
From (i) and (ii), FE || AC ….(iii) [Alternate angles are equal]
Also, FG = EG [By construction]
⇒ G lies on the perpendicular bisector of EF in
⇒ angle GIE = 900 … (iv)
So, angle GAB = angle GIE = 900 [Corresponding angles]
GF = GE [Arcs of equal radii]
Question : 2: Construct an angle of 450 at the initial point of a given ray and justify the construction.
Answer :
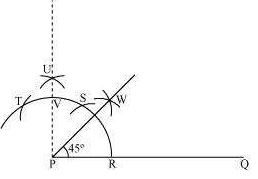
The below given steps will be followed to construct an angle of 450.
(i) Take the given ray PQ. Draw an arc of some radius taking point P as its centre, which
intersects PQ at R.
(ii) Taking R as centre and with the same radius as before, draw an arc intersecting the
previously drawn arc at S.
(iii) Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T
Mddle block 1
(iv) Taking S and T as centre, draw an arc of same radius to intersect each other at U.
(vi) From R and V, draw arcs with radius more than RV/2 to intersect each other at W.
Join PW.
PW is the required ray making 450 with PQ.
Justification of Construction: We can justify the construction, if we can prove ∠WPQ = 450.
For this, join PS and PT.
We have, ∠SPQ = ∠TPS = 600.
In (iii) and (iv) steps of this construction, PU was drawn as the bisector of ∠TPS.
So, ∠UPS = ∠TPS/2 = 600/2 = 300
Also, ∠UPQ = ∠SPQ + ∠UPS
In step (vi) of this construction, PW was constructed as the bisector of ∠UPQ.
So, ∠WPQ = ∠UPQ/2 = 900/2 = 450
Question : 3: Construct the angles of the following measurements:
(i) 300 (ii) 22.50 (iii) 150
Answer :
(i) 300
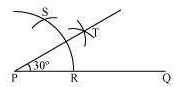
The below given steps will be followed to construct an angle of 300.
Step I: Draw the given ray PQ. Taking P as centre and with some radius, draw an arc of a circle
which intersects PQ at R.
Step II: Taking R as centre and with the same radius as before, draw an arc intersecting the
previously drawn arc at point S.
Step III: Taking R and S as centre and with radius more than RS/2, draw arcs to intersect each
other at T. Join PT which is the required ray making 30° with the given ray PQ.
(ii)22.50
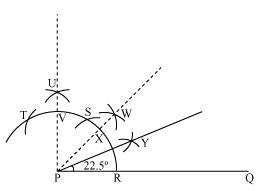
The below given steps will be followed to construct an angle of .
(1) Take the given ray PQ. Draw an arc of some radius, taking point P as its centre,
(2) Taking R as centre and with the same radius as before, draw an arc intersecting the
previously drawn arc at S.
(3) Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T.
(4) Taking S and T as centre, draw an arc of same radius to intersect each other at U.
(5) Join PU. Let it intersect the arc at point V.
(6) From R and V, draw arcs with radius more than RV/2 to intersect each other at W.
Join PW.
(7) Let it intersect the arc at X. Taking X and R as centre and radius more than RX/2, draw arcs
to intersect each other at Y.
Joint PY which is the required ray making with the given ray PQ.
(iii) 150
The below given steps will be followed to construct an angle of 150.

Step I: Draw the given ray PQ. Taking P as centre and with some radius, draw an arc of a circle
which intersects PQ at R.
Step II: Taking R as centre and with the same radius as before, draw an arc.
Step III: Taking R and S as centre and with radius more than RS/2, draw arcs to intersect each
other at T. Join PT.
Step IV: Let it intersect the arc at U. Taking U and R as centre and with radius more than RU/2,
draw an arc to intersect each other at V.
Join PV which is the required ray making 150 with the given ray PQ.
Question : 4: Construct the following angles and verify by measuring them by a protractor:
(i) 750 (ii) 1050 (iii) 1350
Answer :
(i) 750
The below given steps will be followed to construct an angle of 750.
(1) Take the given ray PQ. Draw an arc of some radius taking point P as its centre, which
intersects PQ at R.
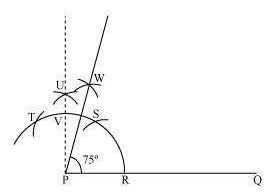
(2) Taking R as centre and with the same radius as before, draw an arc intersecting the
previously drawn arc at S.
(3) Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T.
(4) Taking S and T as centre, draw an arc of same radius to intersect each other at U.
(5) Join PU. Let it intersect the arc at V. Taking S and V as centre, draw arcs with the angle so
formed can be measured with the help of a protractor. It comes to be 750.
(ii) 1050
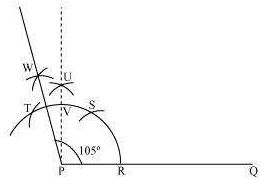
The below given steps will be followed to construct an angle of 1050.
(1) Take the given ray PQ. Draw an arc of some radius taking point P as its centre, which
intersects PQ at R.
(2) Taking R as centre and with the same radius as before, draw an arc intersecting the
previously drawn arc at S.
(3) Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T.
(4) Taking S and T as centre, draw an arc of same radius to intersect each other at U.
(5) Join PU. Let it intersect the arc at V. Taking T and V as centre, draw arcs with radius more
than TV/2. Let these arcs intersect each other at W.
Join PW which is the required ray making 1050 with the given ray PQ.
The angle so formed can be measured with the help of a protractor. It comes to be 1050.
(iii) 1350
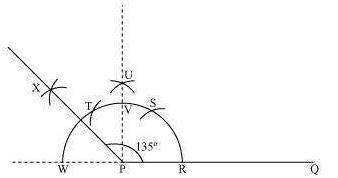
The below given steps will be followed to construct an angle of 1350.
(1) Take the given ray PQ. Extend PQ on the opposite side of Q. Draw a semi-circle of some
radius taking point P as its centre, which intersects PQ at R and W.
(2) Taking R as centre and with the same radius as before, draw an arc intersecting the
previously drawn arc at S.
(3) Taking S as centre and with the same radius as before, draw an arc intersecting the arc at T.
(4) Taking S and T as centre, draw an arc of same radius to intersect each other at U.
(5) Join PU. Let it intersect the arc at V. Taking V and W as centre and with radius more than
VW/2, draw arcs to intersect each other at X.
Join PX, which is the required ray making 1350 with the given line PQ.
The angle so formed can be measured with the help of a protractor. It comes to be 1350.
Question : 5: Construct an equilateral triangle, given its side and justify the construction.
Answer :
Let us draw an equilateral triangle of side 5 cm. We know that all sides of an equilateral
triangle are equal. Therefore, all sides of the equilateral triangle will be 5 cm. We also know
that each angle of an equilateral triangle is 600.
The below given steps will be followed to draw an equilateral triangle of 5 cm side.
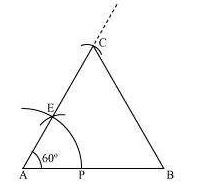
Step I: Draw a line segment AB of 5 cm length. Draw an arc of some radius, while taking A as its
centre. Let it intersect AB at P.
Step II: Taking P as centre, draw an arc to intersect the previous arc at E. Join AE.
Step III: Taking A as centre, draw an arc of 5 cm radius, which intersects extended line segment
AE at C. Join AC and BC.
∆ABC is the required equilateral triangle of side 5 cm.
Justification of Construction: We can justify the construction by showing ABC as an equilateral triangle i.e., AB = BC = AC = 5
cm and ∠A = ∠B = ∠C = 600.
In ∆ABC, we have AC = AB = 5 cm and ∠A = 600.
Since AC = AB, ∠B = ∠C [Angles opposite to equal sides of a triangle]
In ∆ABC,
∠A + ∠B + ∠C = 180° [Angle sum property of a triangle]
∠ 600 + ∠C + ∠C = 1800
∠ 600 + 2 ∠C = 1800
2∠C = 1800− 600 = 1200
∠C = 1200/2
∠C = 600
∠B = ∠C = 600
We have, ∠A = ∠B = ∠C = 600……………..1
So, ∠A = ∠B and ∠A = ∠C
BC = AC and BC = AB [Sides opposite to equal angles of a triangle]
∠ AB = BC = AC = 5 cm ……………………..2
From equations 1 and 2, ∆ABC is an equilateral triangle.

