Class 9 - Mathematics
Lines And Angles - Exercise 6.3

Top Block 1
Exercise 6.3
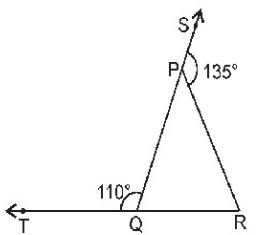
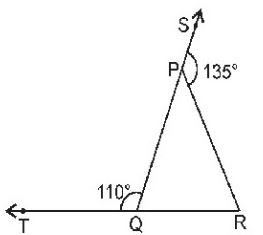
Question : 1 In the figure, sides QP and RQ of ∆ PQR are produced to points S and T respectively. If ∠SPR = 1350 and ∠PQT = 1100, find ∠PRQ.
Answer :
In the given figure, ∠SPR = 1350 and ∠PQT = 1100.
Mddle block 1
∠PQT + ∠PQR = 1800 [Linear pair axiom]
⇒ 1100 + ∠PQR = 1800
⇒ ∠PQR = 1800– 1100 = 700
Also, ∠SPR + ∠QPR = 1800 [Linear pair axiom]
⇒ 1350 + ∠QPR = 1800
⇒ ∠QPS = 1800– 1350 = 450
Now, in the triangle PQR
∠PQR + ∠PRQ + ∠QPR = 1800 [Angle sum property of a triangle]
⇒ 700 + ∠PRQ + 450 = 1800
⇒ ∠PRQ + 1150 = 1800
⇒ ∠PRQ = 1800– 1150 = 650
Hence, ∠ PRQ = 650
Question : 2: In the figure, ∠ X = 620, ∠ XYZ = 540. If YO and ZO are the bisectors of ∠ XYZ and ∠ XZY respectively of
∆ XYZ, find ∠OZY and ∠YOZ.
Answer :
In the given figure,

∠X = 620 and ∠XYZ = 540.
∠XYZ + ∠XZY + ∠YXZ = 1800………1 [Angle sum property of a triangle]
⇒ 540 + ∠XZY + 620 = 1800
⇒ ∠XZY + 1160 = 1800
⇒ ∠XZY = 1800– 1160 = 640
Now, ∠OZY = 1/2 * ∠XZY [Since ZO is bisector of ∠XZY]
= 1/2 * 640 = 320
Similarly, ∠OYZ = 1/2 * 540 = 270
Now, in ∆OYZ, we have
∠OYZ + ∠OZY + ∠YOZ = 1800 [Angle sum property of a triangle]
⇒ 270 + 320 + ∠YOZ = 1800
⇒ ∠YOZ = 1800– 590 = 1210
Hence, ∠OZY = 320 and ∠YOZ = 1210
Question : 3: In the figure, if AB || DE, ∠ BAC = 350 and ∠CDE = 530, find ∠ DCE.
Answer :
In the given figure,
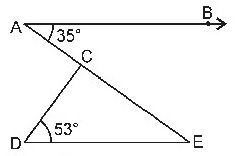
∠BAC = ∠CED [Alternate angles]
⇒ ∠CED = 350
In ∆CDE,
∠CDE + ∠DCE + ∠CED = 1800 [Angle sum property of a triangle]
⇒ 530 + ∠DCE + 350 = 1800
⇒ ∠DCE + 880 = 1800
⇒ ∠DCE = 1800– 880 = 920
Hence, ∠DCE = 920
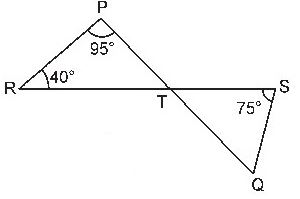
Question : 4: In the figure, if lines PQ and RS intersect at point T, such that ∠ PRT = 400, ∠ RPT = 950
and ∠TSQ = 750, find ∠SQT.
Answer :
In the given figure, lines PQ and RS
intersect at point T, such that ∠PRT = 400,
∠RPT = 950 and ∠TSQ = 750.
In ∆PRT
∠PRT + ∠RPT + ∠PTR = 1800 [Angle sum property of a triangle]
⇒ 400 + 950 + ∠PTR = 1800
⇒ 1350 + ∠PTR = 1800
⇒ ∠PTR = 1800– 1350 = 450
Also, ∠PTR = ∠STQ [Vertical opposite angles]
So, ∠STQ = 450
Now, in ∆STQ,
∠STQ + ∠TSQ + ∠SQT = 180° [Angle sum property of a triangle]
⇒ 450 + 750 + ∠SQT = 1800
⇒ 1200 + ∠SQT = 1800
⇒ ∠SQT = 1800– 1200 = 600
Hence, ∠SQT = 600
Question : 5: In the figure, if PT ⊥ PS, PQ || SR, ∠SQR = 280 and ∠QRT = 650, then find the values of x and y.
Answer :
In the given figure, lines PQ ⊥ PS, PQ || SR,

∠SQR = 280 and ∠QRT = 650
∠PQR = ∠QRT [Alternate angles]
⇒ x + 280 = 650
⇒ x = 650 – 280 = 370
In ∆PQS,
∠SPQ + ∠PQS + ∠QSP = 1800 [Angle sum property of a triangle]
⇒ 900 + 370 + y = 1800 [Since PQ ⊥ PS, ∠PQS = x = 370 and ∠QSP = y)
⇒ 1270 + y = 1800
⇒ y = 1800 – 1270 = 530
Hence, x = 370 and y = 530
Question : 6: In the figure, the side QR of ∆PQR is produced to a point S. If the bisectors of ∠ PQR and ∠ PRS meet at point T, then prove that ∠QTR = ∠QPR/2.
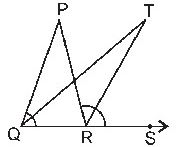
Answer :
Exterior ∠PRS = ∠PQR + ∠QPR [Exterior angle property]
Therefore, ∠PRS/2 = ∠PQR/2 + ∠QPR/2
⇒ ∠TRS = ∠TQR + ∠QPR/2 ……………1
But in ∆QTR,
Exterior ∠TRS = ∠TQR + ∠QTR ……….2 [Exterior angles property]
Therefore, from equation 1 and 2, we get
∠TQR + ∠QTR = ∠TQR + ∠QPR/2
⇒ ∠QTR = ∠QPR/2

