NCERT Solutions Class 9 Mathematics Number System Exercise 1.5

Question : 1:Classify the following numbers as rational or irrational:

(i) 2 – √5                (ii) (3 + √23) – √23            (iii) 2√7/7√7              (iv) 1/√2               (v) 2π

Answer :

(i) 2 – √5         

Since it is a difference of a rational and irrational number,

So, 2 – √5 is an irrational number.         

(ii) (3 + √23) – √23 = 3 + √23 – √23 = 3

Which is a rational number.                   

(iii) 2√7/7√7 = (2 * √7)/(7 * √7) = 2/7

Which is a rational number.                       

(iv) 1/√2

The quotient of rational and irrational is an irrational number.

So, 1/√2 is an irrational number.

(v) 2π

2π = 2 * π = Product of a rational and an irrational (which is an irrational number)

So, 2π is an irrational number.

Question : 2:Simplify each of the following expressions:

(i) (3 + √3)(2 + √2)          (ii) (3 + √3)(3 – √3)          (iii) (√5 + √2)²            (iv) (√5 – √2)( √5 + √2)

Answer :

(i) (3 + √3)(2 + √2) = 3(2 + √2) + √3(2 + √2)  

                               = 3 * 2 + 3 * √2 + √3 * 2 + √3 * √2

                               = 6 + 3√2 + 2√3 + √6     

(ii) (3 + √3)(3 – √3) = 3(3 – √3) + √3(3 – √3)

                                 = 3 * 3 – 3 * √3 + √3 * 3 – √3 * √3

                                 = 9 – 3√3 + 3√3 – 3

                                 = 6            

(iii) (√5 + √2)² = (√5 + √2) (√5 + √2)

                         = √5(√5 + √2) + √2(√5 + √2)

                         = √5 * √5 + √5 * √2 + √2 * √5 + √2 * √2

                         = 5 + √10 + √10 + 2

                         = 7 + 2√10             

(iv) (√5 – √2)(√5 + √2) = √5( √5 + √2) – √2(√5 + √2)

                                       = √5 * √5 + √5 * √2 – √2 * √5 – √2 * √2

                                       = 5 + √10 – √10 – 2

                                       = 3

Question : 3:Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, π = c/d.

This seems to contradict the fact that π is irrational. How will you resolve this contradiction?

Answer :

When we measure the length of a line with a scale or with any other device, we only get an

approximate rational value, i.e. c and d both are irrational.

⇒ c/d is irrational and hence π is irrational.

Thus, there is no contradiction in saying that π is irrational.

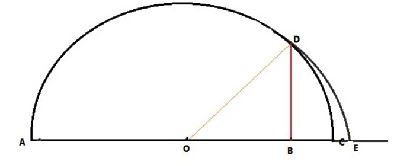
Question : 4:Represent √9.3 on the number line.

Answer :

To represent √9.3 on the number line, draw AB = 9.3 units. Now produce AB to C such that BC

= 1. Draw the perpendicular bisector of AC which intersects AC to O. Taking O as center and

OA as radius, draw a semi-circle which intersects D to the perpendicular at B. Now taking O as

center and OD as radius, draw an arc which intersects AC produced at E.

Hence, OE = √9.3