Class 9 - Mathematics
Probability - Exercise 15.1

Top Block 1
Exercise 15.1
Question : 1: In an ODI match, a wicket keeper drops a catch 6 times out of 30 catches he gets. Find the probability of the wicketkeeper not dropping a catch.
Answer :
Let E be the event of dropping a catch
P(E) = Probability of the wicketkeeper dropping a catch = 6/30 = 1/5
Thus, Probability of not dropping a catch is 1 – P(E) = 1 – 1/5 = 4/5
Question : 2: 1500 families with 2 children were selected randomly, and the following data were recorded:

- 2 girls ii. 1 girl iii. No girl
Also check whether the sum of these probabilities is 1.
Answer :
Total number of families = 475 + 814 + 211 = 1500
- P(Probability of 2 girls) = No. of family having 2 girls/total no. of girls
= 475/1500
- P(Probability of 1 girl) = No. of family having 1 girl/total no. of girls
= 814/1500
iii.P(Probability of No girl) = No. of family having no girl/total no. of girls
= 211/1500
Sum of all Probabilities = P(Probability of 2 girls) + P(Probability of 1 girl) + P(Probability of No
girl)
= 475/1500 + 814/1500 + 211/1500
= (475 + 814 + 211)/1500
= 1500/1500
= 1
Hence, the sum of these probabilities is 1.
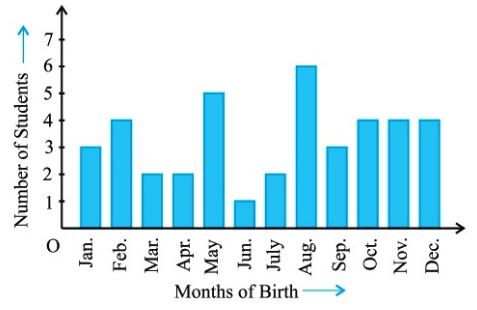
Question : 3: Refer to Example 5, Section 14.4, Chapter 14. Find the probability that a student of the class was born in August.
Mddle block 1
Answer :
Total number of students = 40
Number of students born in August = 6
P( Student born in August) = Number of students born in August/Total number of students
= 6/40
= 3/20
Question : 4: Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes:

Answer :
Total number of times the coins were tossed = 200
Number of times 2 heads occur = 72
So, P(2 heads coming up) = 72/200 = 9/25
Question : 5: An organization selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family.
The information gathered is listed in the table below:

(i) earning Rs 10000 – 13000 per month and owning exactly 2 vehicles.
(ii) earning Rs 16000 or more per month and owning exactly 1 vehicle.
(iii) earning less than Rs 7000 per month and does not own any vehicle.
(iv) earning Rs 13000 – 16000 per month and owning more than 2 vehicles.
(v) owning not more than 1 vehicle.
Answer :
Total number of families: 2400
(i) P( Earning Rs 10000-13000 per month and owning exactly 2 vehicle) = 29/2400
(ii) P( Earning Rs 16000 or more per month and owning exactly 1 vehicle) = 579/2400
= 193/800
(iii) P( Earning less than Rs 7000 per month and does not own any vehicle) = 10/2400
= 1/240
(iv) P(Earning Rs 13000 – 16000 per month and owning more than 2 vehicles) = 25/2400
= 1/96
(v) P(owning not more than 1 vehicle) = P(a family owning 0 vehicle or 1 vehicle)
= (10 + 0 + 1 + 2 + 1 + 160 + 305 + 535 + 469 + 579)/2400
= 2062/2400 = 1031/1200
Question : 6: Refer to Table 14.7, Chapter 14.

(ii) Find the probability that a student obtained marks 60 or above
Answer :
Total number of students = 90
(i) P(a student obtained less than 20%)
= No. of student obtained less than 20%/Total no of students
= 7/90
(ii) P(a student obtained 60 marks or above)
= No. of students who obtained 60 marks or more/Total no. of students
= (15 + 8)/90
= 23/90
Question : 7: To know the opinion of the students about the subject statistics, a survey of 200 students was conducted. The data is recorded in the following table.

(i) likes statistics (ii) does not like it
Answer :
Total number of students = 200
Number of students liking the subject = 135
Number of students disliking the subject = 65
- P(liking the subject) = 135/200 = 27/40
- P(Disliking the subject) = 65/200 = 13/40
Question : 8: Refer to Q.2, Exercise 14.2. What is the empirical probability that an engineer lives:

(ii) more than or equal to 7 km from her place of work?
(iii) within 1/2 km from her place of work?
Answer :
Total number of engineers = 40
Let us arrange the data in ascending order as follows:
2, 2, 3, 3, 3, 5, 5, 6, 6, 7, 7, 7, 7, 8, 9,9, 10, 10, 11, 11, 12, 12, 12, 12, 12, 13, 14, 15, 15, 16, 17,
17, 18, 18, 19, 20, 25, 31, 32
(i) P(an engineer lives less than 7 km from her place of work)
= Number of engineer lives less than 7 km from her place of work/Total no. of engineer
= 9/40
(ii) P(an engineer lives more than or equal to 7 km from their place of work)
= engineer lives more than or equal to 7 km from their place of work /Total no. of engineer
= 31/40
(iii) P(an engineer lives within 1/2 km from her place of work)
= Number of engineer lives within 1/2 km from her place of work/Total no. of engineer
= 0/40 = 0
Note: Questions 9 and 10 are activities, so student should perform it on their own.
Question : 11: Eleven bags of wheat flour, each marked 5 kg, actually contained the following weights of flour (in kg):
4.97 5.05 5.08 5.03 5.00 5.06 5.08 4.98 5.04 5.07 5.00
Find the probability that any of these bags chosen at random contains more than 5 kg of flour.
Answer :
Total number of bags examined = 11
P(a bag weighing more than 5 kg) = No. of bags which weigh more than 5 kg/Total no. of bags
= 7/11
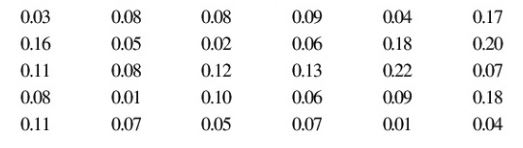
Question : 12: In Q.5, Exercise 14.2, you were asked to prepare a frequency distribution table, regarding the concentration of sulphur dioxide in the air in parts per million of a certain city for 30 days.
Using this table, find the probability of the concentration of sulphur dioxide in the interval 0.12 – 0.16 on any of these days.
Answer :
Total number of students = 30
P(concentration of sulphur dioxide in the interval 0.12 – 0.16 in a day)
= Number of days on which the concentration was in the interval 0.12 – 0.16/Total no. of days
= 2/30
= 1/15

