Class 9 - Mathematics
Surface Areas and Volumes - Exercise 13.7

Top Block 1
Exercise 13.7
Question :1 : Find the volume of the right circular cone with
(i) radius 6 cm, height 7 cm (ii) radius 3.5 cm, height 12 cm.
Answer :
(i) Here, radius of the cone (r) = 6 cm, Height (h) = 7 cm
So, volume = πr2 h/3
= (1/3) * (22/7) * 6 * 6 * 7
= (1/3) * 22 * 6 * 6
= 22 * 6 * 2
= 264 cm3
(ii) Here, radius of cone (r) = 3.5 cm, Height (h) = 12 cm
So, volume = πr2 h/3
= (1/3) * (22/7) * 3.5 * 3.5 * 12
= (1/3) * 22 * 3.5 * 0.5 * 12
= 22 * 3.5 * 0.5 * 4
= 154 cm3
Question : 2: Find the capacity in litres of a conical vessel with
(i) radius 7 cm, slant height 25 cm (ii) height 12 cm, slant height 13 cm
Answer :
(i) Here, r = 7 and I = 25 cm
Now, radius (r) = √(I2 – h2)
= √(132 – 122)
= √(169 – 144)
= √25
⇒ r = 5 cm
Now, volume of conical vessel = πr2 h/3
= (1/3) * (22/7) * 5 * 5 * 12
= (22/7) * 5 * 5 * 4
= 2200/7 cm3
Now, capacity of the conical vessel = (2200/7) * (1/1000) l
= 22/70 l
= 11/35 l
Thus, the required capacity of the conical vessel is 11/35 l.
Question : 3: The height of a cone is 15 cm. If its volume is 1570 cm3, find the radius of the base.
Answer :
Here, height of the cone (h) = 15 cm
Volume of the cone (v) = 1570 cm3
Let the radius of the base be r cm.
⇒ πr2 h/3 = 1570
⇒ (3.14 * r2 * 15)/3 = 1570
⇒ 3.14 * r2 * 5 = 1570
⇒ 15.70 * r2 = 1570
⇒ r2 = 1570/15.70
⇒ r2 = (1570 * 100)/1570
⇒ r2 = 100
⇒ r = √100
⇒ r = 10
Thus, the required radius of the base is 10 cm.
Question : 4: If the volume of a right circular cone of height 9 cm is 48π cm3, find the diameter of its base.
Answer :
Volume of the cone = 48 π cm3
Height of the cone (h) = 9 cm
Let r be its base radius.
⇒ πr2 h/3 = 48π
⇒ (r2 * 9)/3 = 48
⇒ 3r2 = 48
⇒ r2 = 48/3
⇒ r2 = 16
⇒ r = √16
⇒ r = 4
Now, Diameter = 2 * r = 2 * 4 = 8
So, diameter of the base of the cone = 8 cm
Question : 5: A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres?
Answer :
Here, diameter of the conical pit = 3.5 m
Radius (r) = 3.5/2 m, Depth (h) = 12 m
Volume (capacity) = πr2 h/3
= (22/7) * (3.5/2) * (3.5/2) * 12 * (1/3)
= 22 * (0.5/2) * (3.5/2) * 4
= 22 * 0.5 * 3.5
= 38.5 m3
Since 1000 cm3 = 1 l
and 1000000 cm3 = l m3
So, 1000 * 1000 cm3 = 1000 l = 1 kl
Also, 1000 * 1000 cm3 = 1 m3
⇒ 1 m3 = 1 kl
⇒ 38.5 m3 = 38.5 kl
Thus, the capacity of the conical pit is 38.5 kl.
Question : 6: The volume of right circular cone is 9856 cm3. If the diameter of the be is 28 cm, find
(i) height of the cone (ii) slant height of the cone
(iii) curved surface area of the cone.
Answer :
Volume of the cone (v) = 9856 cm3
Diameter of the base = 28 cm
Radius of the base = 28/2 = 14 cm
Volume (capacity) = πr2 h/3
= (1/3) * (22/7) * 14 * 14 * h
= (1/3) * 22 * 2 * 14 * h
Now, (1/3) * 22 * 2 * 14 * h = 9856
⇒ h = (9856 * 3)/(22 * 2 * 14)
⇒ h = 16 * 3
⇒ h = 48 cm
Thus, the required height is 48 cm.
(ii) Let the slant height be l cm.
(Slant height)2 = (Radius)2 + (Height)2
⇒ l2 = 142 + 482
⇒ l2 = 196 + 2304
⇒ l2 = 2500
⇒ l2 = √2500
⇒ l = 50
Thus, the required height = 50 cm.
(iii) To find the curved surface area
The curved surface area of a cone = πrl
= (22/7) * 14 * 50
= 22 * 2 * 50
= 2200
Thus, the curved surface area of the cone is 2200 cm2.
Question : 7: A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
Answer :
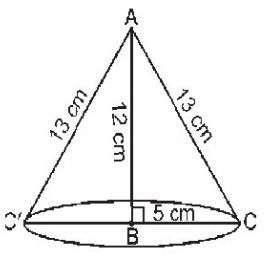
Sides of the right triangle are 5 cm, 12 cm and 13 cm.
Since the right angled triangle is revolved about the 12 cm side.
So, Its height is 12 cm and base is 5 cm.
Thus, we have Radius of the base of the cone so formed (r) = 5 cm
Height (h) = 12 cm, Slant height = 13 cm
Now, volume of the cone so obtained = πr2 h/3
= (1/3) * π * 5 * 5 * 12
= π * 5 * 5 * 4
= 100π cm3
Thus, the required volume of the cone is 100π cm3
Question : 8: If the triangle ABC in the question 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained.
Find also the ratio of the volumes of the two solids obtained in Questions 7 and 8.

Mddle block 1
Answer :
Since the right triangle is revolved about the side 5 cm.
So, Height of the cone so obtained (h) = 5 cm
And radius of the cone (r) = 12 cm
Now, volume of the cone so obtained = πr2 h/3
= (1/3) * π * 12 * 12 * 5
= π * 4 * 12 * 5
= 240π cm3
Now, volume of cone having radius 5 cm/ volume of cone having radius 12 cm
= 100π/240π
= 5/12
= 5 : 12
Thus, the required ratio is 5 : 12
Question : 9: A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain.
Find the area of the canvas required.
Answer :
Here the heap of wheat is in the form of a cone such that
Base diameter = 10.5 m
Base radius (r) = 10.5/2 = 5.25 m
Height (h) = 3 m
Now, volume of heap = πr2 h/3
= (22/7) * 5.25 * 5.25 * 3 * (1/3)
= 22 * 5.25 * 0.75
= 86.625 m3
Thus, the required volume = 86.625 m3
Since, the area of the canvas to cover the heap must be equal to the curved surface area of the
conical heap.
Area of the canvas = πrl
Now, l2 = r2 + h2
⇒ l2 = (5.25)2 + 32
⇒ l2 = 27.5625 + 9
⇒ l2 = 36.5625
⇒ l2 = √36.5625
⇒ l = 6.046
⇒ l = 6.05 (approx.)
Now, Area of the canvas = πrl
= (22/7) * 5.25 * 6.05
= 22 * 0.75 * 6.05
= 99.825 m2
Thus, the required area of the canvas is 99.825 m2.

