Class 9 - Mathematics
Triangles - Exercise 7.2

Top Block 1
Exercise 7.2
Question : 1 : In an isosceles triangle ABC, with AB = AC, the bisectors of ∠ B and ∠ C intersect each other at O. Join A to O. Show that:
(i) OB = OC (ii) AO bisects ∠ A

Answer :
(i) In ΔABC, we have
AB = AC [Given]
∠C = ∠B [Angle opposite to equal sides are equal]
∠OCB = ∠OBC
⇒ OB = OC [Sides opposite to equal angles are equal
(ii) In ΔABO and ΔACO, we have
AB = AC [Given]
OB = OC [Proved]
Using SAS criteria,
ΔABO ≌ΔACO
⇒ ∠OAB = ∠OAC [By CPCT]
⇒ AO bisects ∠A.
Question : 2: In Δ ABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that Δ ABC is an isosceles triangle in which AB = AC.

Mddle block 1
Answer :
Since AD is bisector of BC.
So, BD = CD
Now, in ΔABD and ΔACD, we have:
AD = AD [Common]
∠ADB = ∠ADC = 900 [Since AD ⊥ BC]
BD = CD [Proved]
So, ΔABD ≌ΔACD [SAS criteria]
Hence, their corresponding parts are equal.
⇒ AB = AC
Thus, ΔABC is an isosceles triangle.
Question : 3: ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31).
Show that these altitudes are equal.

Answer :
ΔABC is an isosceles triangle. So, AB = AC
⇒ ∠ACB = ∠ABC [Since angles opposite to equal sides are equal]
Now, in ΔBEC and ΔCFB, we have
∠EBC = ∠FCB [Proved]
BC = CB [Common]
and ∠BEC = ∠CFB [Each = 900]
So, ΔBEC ≌ΔCFB [Using ASA criteria]
⇒ Their corresponding parts are equal. i.e. BE = CF
Question : 4: ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32).
Show that
(i) Δ ABE ≅Δ ACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.

Answer :
(i) In ΔABE and ΔACF, we have
∠AEB = ∠AFC [each = 900 since BE ⊥AC and CF ⊥ AB]
∠A = ∠A [Common]
BE = CF [Given]
So, ΔABE ≌ΔACF [Using AAS criterion]
(ii) Since, ABE ≌ΔACF
So, their corresponding parts are equal.
⇒ AB = AC
Question : 5: ABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that ∠ ABD = ∠ ACD.
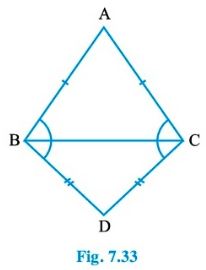
Answer :
In ΔABC, we have
AB = AC [Since ΔABC is an isosceles triangle]
But angles opposite to equal sides are equal.
So, ∠ABC = ∠ACB ……….(1)
Again, in ΔBDC, we have
BD = CD [Since ΔBDC is an isosceles triangle.]
So, ∠CBD = ∠BCD …….(2) [Angles opposite to equal sides are equal]
Adding equation (1) and (2), we have
∠ABC + ∠CBD = ∠ACB + ∠BCD
⇒ ∠ABD = ∠ACD
Question : 6: ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB
(see Fig. 7.34). Show that ∠ BCD is a right angle.
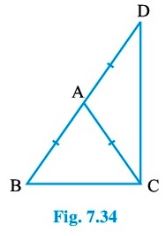
Answer :
In ΔABC,
AB = AC [Given] …….(1)
AB = AD [Given] …….(2)
From equation (1) and (2), we have
AC = AD
Now, in ΔABC, we have
∠B + ∠ACB + ∠BAC = 1800
⇒ 2∠ACB + ∠BAC = 1800 ……..(3) [Since ∠B = ∠ACB (Angles opposite to equal sides)]
In ΔACD,
∠D + ∠ACD + ∠CAD = 1800
⇒ 2∠ACD + ∠CAD = 1800 …….(4) [Since ∠D = ∠ACD (angles opposite to equal sides)]
Adding equations (3) and (4), we have
2∠ACB + ∠BAC + 2∠ACD + ∠CAD = 1800 + 1800
⇒ 2[∠ACB + ∠ACD] + [∠BAC + ∠CAD] = 3600
⇒ 2[∠BCD] + [1800] = 3600 [∠BAC and ∠CAD form a linear pair]
⇒ 2∠BCD = 3600– 1800 = 1800
⇒ ∠BCD = 1800/2 = 900
Thus, ∠BCD = 900
Question : 7: ABC is a right angled triangle in which ∠ A = 900 and AB = AC. Find ∠ B and ∠ C.
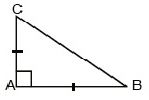
Answer :
In ΔABC, we have
AB = AC [Given]
So, their opposite angles are equal.
⇒ ∠ACB = ∠ABC
Now, ∠A + ∠B + ∠C = 1800
⇒ 900 + ∠B + ∠C = 1800 [Since ∠A = 900 (Given)]
⇒ ∠B + ∠C = 1800 – 900
⇒ ∠B + ∠C = 900
But ∠ABC = ∠ACB, i.e. ∠B = ∠C
Thus, ∠B = 450 and ∠C = 450
Question : 8: Show that the angles of an equilateral triangle are 600 each.
Answer :
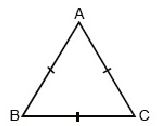
In ΔABC, we have
AB = BC = CA [Since ABC is an equilateral triangle]
⇒ AB = BC
⇒ A = ∠C ………(1) [Since Angle opposite to equal sides are equal.]
Similarly, AC = BC
⇒ ∠A = ∠B …….(2)
From equation (1) and (2), we have
∠A = ∠B = ∠C
Let ∠A = ∠B = ∠C = x
Since, ∠A + ∠B + ∠C = 1800
⇒ x + x + x = 1800
⇒ 3x = 1800
⇒ x = 1800/3
⇒ x = 600
Thus, the angles of an equilateral triangle are 600 each.

