Class 9 - Mathematics
Triangles - Exercise 7.4

Top Block 1
Exercise 7.4
Question : Show that in a right angled triangle, the hypotenuse is the longest side.
Answer :

Let us consider ΔABC such that ∠B = 900
So, ∠A + ∠B + ∠C = 1800
⇒ [∠A + ∠C] + ∠B = 1800
⇒ ∠A + ∠C = ∠B
⇒ ∠B > ∠A and ∠B > ∠C
⇒ Side opposite to ∠B is longer than the side opposite to ∠A.
i.e. AC > BC …….(1)
Similarly, AC > AB …….(2)
From equation (1) and (2), we get,
AC is the longest side.
But AC is the hypotenuse of the triangle.
Thus, hypotenuse is the longest side.
Question : 2: In Fig. 7.48, sides AB and AC of Δ ABC are extended to points P and Q respectively.
Also, ∠ PBC < ∠ QCB. Show that AC > AB.
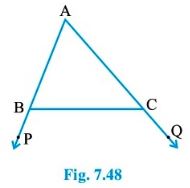
Answer :
∠ABC + ∠PBC = 1800 [Linear pair]
∠ACB + ∠QCB = 1800 [Linear pair]
So, ∠ABC + ∠PBC = ∠ACB + ∠QCB
But ∠PBC < ∠QCB [Given]
So, ∠ABC > ∠ACB
⇒ [The side opposite to ∠ABC] > [The side opposite to ∠ACB]
⇒ AC > AB
Question : 3: In Fig. 7.49, ∠ B < ∠ A and ∠ C < ∠ D.Show that AD < BC.

Mddle block 1
Answer :
Given ∠B < ∠A
⇒ ∠A > ∠B
So, OB > OA [Since side opposite to greater angle is longer]……..(1)
Similarly,
OC > OD…………(2)
From equation (1) and (2), we have
[OB + OC] > [OA + OD]
⇒ BC > AD
Question : 4: AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD
(see Fig. 7.50). Show that ∠ A > ∠ C and ∠ B > ∠ D.

Answer :
Let us join AC.
Now, in ΔABC,
AB < BC [Since AB is the smallest side of quadrilateral ABCD]
⇒ BC > AB
⇒ [Angle opposite to BC] < [Angle opposite to AB]
⇒ ∠BAC > ∠BCA ………..(1)
Again, in ΔACD,
CD > AD [Since CD is the longest side of the quadrilateral ABCD]
⇒ [Angle opposite to CD] > [Angle opposite to AD]
⇒ ∠CAD > ∠ACD ……….(2)
Adding equation (1) and (2), we get
[∠BAC + CAD] > [∠BCA + ∠ACD]
⇒ ∠A > ∠C
Similarly, by joining BD, we have
∠B > ∠D
Question : 5: In Fig 7.51, PR > PQ and PS bisects ∠ QPR. Prove that ∠ PSR > ∠ PSQ
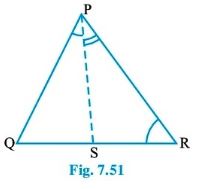
Answer :
In ΔPAR, PS bisects ∠QPR [Given]
So, ∠QPS = ∠RPS
Again PR > PQ [Given]
⇒ [Angle opposite to PR] > [Angle opposite to PQ]
⇒ ∠PQS > ∠PRS
⇒ [∠PQS + ∠QPS] > [∠PRS + ∠RPS] …….(1) [Since ∠QPS = ∠RPS]
So, Exterior ∠PSR = [∠PQS + ∠QPS]
[An exterior angle is equal to the sum of interior opposite angles]
And Exterior ∠PSQ = [∠PRS + ∠RPS]
Now, from (1), we have
∠PSR > ∠PSQ
Question : 6: Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
Answer :

Let we have a line l and O is a point not on line l such that OP Ʇ l.
We have to prove that OP < OQ, OP < OR and OP < OS.
In ΔOPQ,
∠P = 900
So, ∠Q is an acute angle i.e. ∠Q < 900
So, ∠Q < ∠P
Hence, OP < OQ [Side opposite to greater angle is longer]
Similarly, we can prove that OP is shorter than OR, OS.

