Class 10 - Mathematics
Linear Equations In Two Variables - Exercise 3.1

Top Block 1
Exercise 3.1
Question : 1:Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then.
Also, three years from now, I shall be three times as old as you will be.” (Isn’t this interesting?)
Represent this situation algebraically and graphically.
Answer :
Let the present age of Aftab = x
and present age of his daughter is represented as = y
Seven years ago,
Aftab’s age = x – 7
Age of Aftab’s daughter = y – 7
According to the question,
(x – 7) = 7 (y – 7 )
⇒ x – 7 = 7 y – 49
⇒ x – 7y = – 49 + 7
⇒ x – 7y = – 42 … (i)
⇒ x = 7y – 42
⇒ Putting y = 5, 6 and 7, we get
⇒ x = 7 * 5 – 42 = 35 – 42 = – 7
⇒ x = 7 * 6 – 42 = 42 – 42 = 0
⇒ x = 7 * 7 – 42 = 49 – 42 = 7
|
x |
-7 |
0 |
7 |
|
y |
5 |
6 |
7 |
Three years from now,
Aftab’s age = x + 3
Age of Aftab’s daughter = y + 3
According to the question,
(x + 3) = 3 (y + 3)
⇒ x + 3 = 3y + 9
⇒ x – 3y = 9 – 3
⇒ x – 3y = 6 … (ii)
⇒ x = 3y + 6
⇒ Putting, y = – 2, –1 and 0, we get
⇒ x = 3 * (-2) + 6 = – 6 + 6 =0
⇒ x = 3 * (-1) + 6 = – 3 + 6 = 3
⇒ x = 3 * 0 + 6 = 0 + 6 = 6
|
x |
0 |
3 |
6 |
|
y |
-2 |
-1 |
0 |
From equation (i) and (ii)
x – 7y = – 42 … (i)
x – 3y = 6 … (ii)
Graphical representation is given as above.
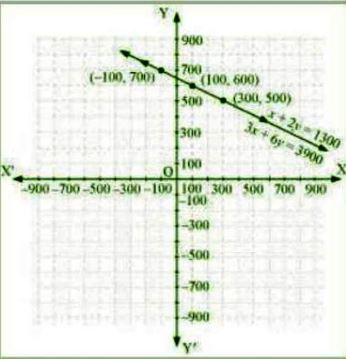
Question : 2:The coach of a cricket team buys 3 bats and 6 balls for Rs 3900. Later, she buys another bat and 2 more balls of the same kind for Rs 1300.
Represent this situation algebraically and geometrically.
Answer :
Let the cost of one bat = Rs x
Let the cost of one ball = Rs y
According to first condition,
3x + 6y = 3900 …………..1
According to second condition,
x + 2y = 1300 …………….2
Hence, the following is the algebraic
representation of the situation:
3x + 6y = 3900
x + 2y = 1300
Now, for graphical representation, the three solutions of each equation are as follows:
From equation 1, we get
y = (3900 – 3x)/6
|
x |
300 |
100 |
-100 |
|
y |
500 |
600 |
700 |
From equation 2, we get
y = (1300 – x)/2
|
x |
300 |
100 |
-100 |
|
y |
500 |
600 |
700 |
Mddle block 1
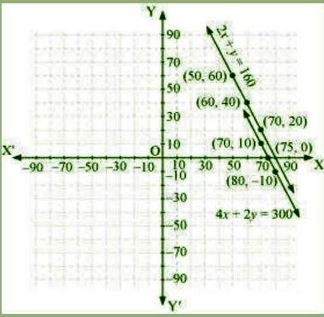
Question : 3:The cost of 2 kg of apples and 1kg of grapes on a day was found to be Rs 160.
After a month, the cost of 4 kg of apples and 2 kg of grapes is Rs 300.
Represent the situation algebraically and geometrically.
Answer :
Let the cost of 1 kg of apple = Rs x
Let the cost of 1 kg of grapes = Rs y
According to first condition,
2x + y = 160 …………..1
According to second condition,
4x + 2y = 300 …………….2
Hence, the following is the algebraic
representation of the situation:
2x + y = 160
4x + 2y = 300
Now, for graphical representation, the three solutions of each equation are as follows:
From equation 1, we get
y = 160 – 2x
|
x |
50 |
60 |
70 |
|
y |
60 |
40 |
20 |
From equation 2, we get
y = (300 – 4x)/2
|
x |
70 |
80 |
75 |
|
y |
10 |
-10 |
0 |