Class 10 - Mathematics
Polynomials - Exercise 2.3

Top Block 1
Exercise 2.3
Question : 1:Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following:
(i) p(x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2 (ii) p(x) = x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x
(iii) p(x) = x4 – 5x + 6, g(x) = 2 – x2
Answer :
(i) p(x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2

(ii) p(x) = x4 – 3x2 + 4x + 5, g(x) = x2 + 1 – x

Mddle block 1
(iii) p(x) = x4 – 5x + 6, g(x) = 2 – x2

Question : 2:Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
(i) t2 – 3, 2t4 + 3t3 – 2t2 – 9t – 12 (ii) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
(iii) x3 – 3x + 1, x5 – 4x3 + x2 + 3x + 1
Answer :
(i) t2 – 3, 2t4 + 3t3 – 2t2 – 9t – 12
Since remainder is 0
Hence t2 – 3 is a factor of 2t4 + 3t3 – 2t2 – 9t – 12


(iii) x3 – 3x + 1, x5 – 4x3 + x2 + 3x + 1

Question : 3:Obtain all other zeroes of 3x4 + 6x3 – 2x2 – 10x – 5, if two of its zeroes are √(5/3) and – √(5/3)
Answer :

Let x = √√(5/3) and x = -√(5/3)⇒ x – √(5/3) = 0 and x + √(5/3) = 0
⇒ {x – √(5/3)}{x + √(5/3)} = 0
⇒ x2 – 5/3 = 0
⇒ 3x2 – 5 = 0
Apply division lemma, we get
Quotient = x2 + 2x + 1 and remainder = 0
So, 3x2 – 5 is a factor of 3x4 + 6x3 – 2x2 – 10x – 5
Now, 3x4 + 6x3 – 2x2 – 10x – 5 = (3x2 – 5)(x2 + 2x + 1)
= 3(x2 – 5/3)(x2 + 2x + 1)
= 3{x – √(5/3)}{x + √(5/3)} (x + 1)2
= 3{x – √(5/3)}{x + √(5/3)} (x + 1)(x + 1)
Hence, the zeroes are: -1, -1, √(5/3) and -√(5/3)
Question : 4:On dividing x3 – 3x2 + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and -2x + 4, respectively. Find g(x).
Answer :
According to division algorithm,
Dividend = Divisor * Quotient+ Remainder
⇒ p(x) = g(x) * q(x) + r(x),
Put the value in formula we get
x3 – 3x2 + x + 2 = g(x) *(x – 2) – 2x + 4
Add 2x and subtract 4 both side we get
x3 – 3x2 + x + 2 + 2x – 4 = g(x) *(x – 2)
⇒ g(x) = (x3 – 3x2 + 3x– 2)/(x – 2)
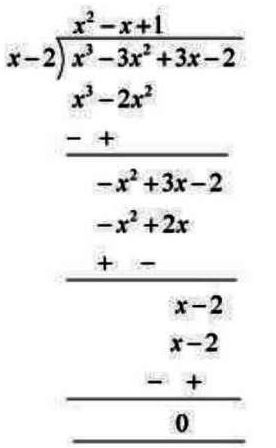
Question : 5:Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x) (ii) deg q(x) = deg r(x) (iii) deg r(x) = 0
Answer :
According to the division algorithm,
if p(x) and g(x) are two polynomials with g(x) ≠ 0,
then we can find polynomials q(x) and r(x) such that p(x) = g(x) * q(x) + r(x),
where r(x) = 0 or degree of r(x) < degree of g(x)
Degree of a polynomial is the highest power of the variable in the polynomial.
(i) deg p(x) = deg q(x)
Degree of quotient will be equal to degree of dividend when divisor is constant i.e. when any
polynomial is divided by a constant.
Let us assume the division of 6x2 + 2x + 2 by 2
Here, p(x) = 6x2 + 2x + 2, g(x) = 2
q(x) = 3x2 + x + 1 and r(x) = 0
Degree of p(x) and q(x) is the same i.e. 2
Checking for division algorithm, p(x) = g(x) * q(x) + r(x)
6x2 + 2x + 2 = 2(3x2 + x + 1) + 0
Thus, the division algorithm is satisfied.
(ii) deg q(x) = deg r(x)
Let us assume the division of x3 + x by x2
Here, p(x) = x3 + x, g(x) = x2, q(x) = x and r(x) = x
Clearly, the degree of q(x) and r(x) is the same i.e. 1
Checking for division algorithm, p(x) = g(x) * q(x) + r(x)
x3 + x = x2 * x + x = x3 + x
Thus, the division algorithm is satisfied.
(iii) deg r(x) = 0
Degree of remainder will be 0 when remainder comes to a constant.
Let us assume the division of x3 + 1 by x2
Here, p(x) = x3 + 1, g(x) = x2, q(x) = x and r(x) = 1
Clearly, the degree of r(x) is 0
Checking for division algorithm,
p(x) = g(x) * q(x) + r(x)
x3 + 1 = x2 * x + 1 = x3 + 1
Thus, the division algorithm is satisfied.

