Class 10 - Mathematics
Triangles - Exercise 6.6

Top Block 1
Exercise 6.6
Question : 1:In Fig. 6.56, PS is the bisector of ∠ QPR of Δ PQR. Prove that QS/SR = PQ/PR.
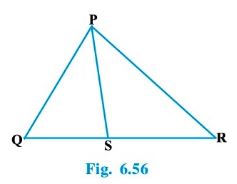
Answer :
Line RT is drawn parallel to SP which intersects QP produced at T.
Given that SP bisects angle QPR, therefore
∠ QPS = ∠ SPR ……….1
By construction,
∠ SPR = ∠ PRT (As PS || TR) ……….2
∠ QPS = ∠ QTR (As PS || TR) ……….3
From the above equations, we have
∠ PRT = ∠ QTR
So, PT = PR
By construction, PS || TR
In ΔQTR, by Thales theorem,
QS/SR = QP/PT
⇒ QS/SR = PQ/QR [Since PT = TR]
Mddle block 1
Question : 2:In Fig. 6.57, D is a point on hypotenuse AC of Δ ABC, DM ⊥ BC and DN ⊥ AB. Prove that:
(i) DM2 = DN . MC (ii) DN2 = DM . AN
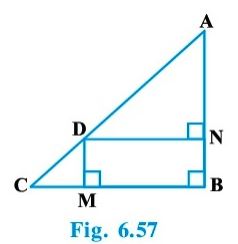
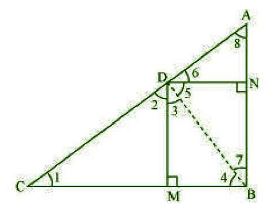
Answer :
(i) Join B and D.
Given that DN || CB, DM || AB and ∠ B = 90.
So, DMBN is a rectangle.
Given that BD Ʇ AC,
So, ∠ CDB = 90
⇒ ∠ 2 + ∠ 3 = 90 …………..1
In ΔCDM,
∠ 1 + ∠ 2 + ∠ DMC = 180
⇒ ∠ 1 + ∠ 2 = 180 – ∠ DMC
⇒ ∠ 1 + ∠ 2 = 180 – 90
⇒ ∠ 1 + ∠ 2 = 90 …….2
In ΔDMB,
∠ 2 + ∠ DMB + ∠ 4 = 180
⇒ ∠ 2 + ∠ 4 = 180 – ∠ DMB
⇒ ∠ 2 + ∠ 4 = 180 – 90
⇒ ∠ 2 + ∠ 4 = 90 …….3
From equation 1 and 2, we get
∠ 1 = ∠ 3
From equation 1 and 3, we get
∠ 2 = ∠ 4
In ΔDCM and ΔBDM,
∠ 1 = ∠ 3 [Proved]
∠ 2 = ∠ 4 [Proved]
So, Δ DCM ~ Δ BDM [AAA similarity]
⇒ BM/DM = DM/MC
⇒ DN/DM = DM/MC [Since BM = DN]
⇒ DM2 = DN * MC
(ii) In ΔDBN,
∠ 5 + ∠ 7 = 90 …………4
In ΔDAN,
∠ 6 + ∠ 8 = 90 …………5
But, BD Ʇ AC
So, ∠ ADB = 90
⇒ ∠ 5 + ∠ 6 = 90 …………6
From equation 4 and 6, we have ∠ 6 = ∠ 7
From equation 4 and 6, we have ∠ 8 = ∠ 5
In ΔDNA and ΔBND,
∠ 6 = ∠ 7 [Proved]
∠ 8 = ∠ 5 [Proved]
So, Δ DNA ~ Δ BND [AA similarity]
⇒ AN/DN = DN/NB
⇒ DN2 = AN * NB
⇒ DN2 = AN * DM [Since NB = DM]
Question : 3:In Fig. 6.58, ABC is a triangle in which ∠ ABC > 90° and AD ⊥ CB produced. Prove that
AC2 = AB2 + BC2 + 2 BC . BD.
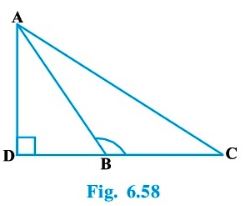
Answer :
In ΔADB, By Pythagoras theorem,
AB2 = AD2 + DB2 ………..1
In ΔACD, By Pythagoras theorem,
AC2 = AD2 + DC2
⇒ AC2 = AD2 + (DB + BC) 2
⇒ AC2 = AD2 + DB2 + BC2 + 2 * DB * BC
⇒ AC2 = AB2 + BC2 + 2DB * BC [From equation 1]
Question : 4:In Fig. 6.59, ABC is a triangle in which ∠ ABC > 90° and AD ⊥ CB produced.
Prove that AC2 = AB2 + BC2 + 2 BC . BD
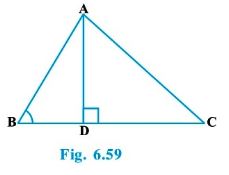
Answer :
In ΔADB, By Pythagoras theorem,
AB2 = AD2 + DB2
⇒ AD2 = AB2 – DB2 ………..1
In ΔACD, By Pythagoras theorem,
AC2 = AD2 + DC2
⇒ AC2 = AB2 – DB2 + DC 2 [From equation 1]
⇒ AC2 = AB2 – DB2 + (BC – BD) 2
⇒ AC2 = AB2 – DB2 + BC2 + BD2 – 2BC * BD
⇒ AC2 = AB2 + BC2 – 2BC * BD
Question : 5:In Fig. 6.60, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:
(i) AC2 = AD2 + BC . DM + (BC/2)2
(ii) AB2 = AD2 – BC . DM + (BC/2)2
(ii) AC2 + AB2 = 2AD2 + BC2/2
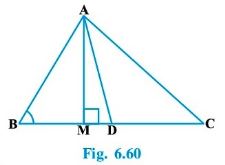
Answer :
(i) Applying Pythagoras theorem in ΔAMD, we obtain
AM2 + MD2 = AD2 ……… (1)
Applying Pythagoras theorem in ΔAMC, we obtain
AM2 + MC2 = AC2
AM2 + (MD + DC) 2 = AC2
(AM2 + MD2) + DC2 + 2MD.DC = AC2
AD2 + DC2 + 2MD.DC = AC2 [Using equation (1)]
Using the result DC = BC/2, we obtain
AD2 + (BC/2)2 + 2MD.(BC/2) = AC2
AD2 + (BC/2)2 + MD.BC = AC2
(ii) Applying Pythagoras theorem in ΔABM, we obtain
AB2 = AM2 + MB2
= AD2 − DM2 + MB2
= AD2 − DM2 + (BD − MD)2
= AD2 − DM2 + BD2 + MD2 − 2BD * MD
= AD2 + BD2 − 2BD * MD
= AD2 + (BC/2)2 – 2(BC/2) * MD
= AD2 + (BC/2)2 – BC * MD
(iii)Applying Pythagoras theorem in ΔABM, we obtain
AM2 + MB2 = AB2 ……… (1)
Applying Pythagoras theorem in ΔAMC, we obtain
AM2 + MC2 = AC2 …….… (2)
Adding equations (1) and (2), we obtain
2AM2 + MB2 + MC2 = AB2 + AC2
⇒ 2AM2 + (BD − DM) 2 + (MD + DC) 2 = AB2 + AC2
⇒ 2AM2 +BD2 + DM2 − 2BD.DM + MD2 + DC2 + 2MD.DC = AB2 + AC2
⇒ 2AM2 + 2MD2 + BD2 + DC2 + 2MD (− BD + DC) = AB2 + AC2
⇒ 2(AM2 + MD2) + (BC/2)2 + (BC/2)2 + 2MD (− BC/2 + BC/2) = AB2 + AC2
⇒ 2AD2 + BC2/2 = AB2 + AC2
Question : 6:Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
Answer :
Let ABCD be a parallelogram.
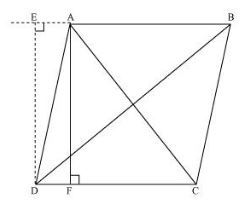
Applying Pythagoras theorem in ΔDEA, we obtain
DE2 + EA2 = DA2 ……..… (i)
Applying Pythagoras theorem in ΔDEB, we obtain
DE2 + EB2 = DB2
DE2 + (EA + AB)2 = DB2
(DE2 + EA2) + AB2 + 2EA * AB = DB2
DA2 + AB2 + 2EA * AB = DB2 ………… (ii)
Applying Pythagoras theorem in ΔADF, we obtain
AD2 = AF2 + FD2
Applying Pythagoras theorem in ΔAFC, we obtain
AC2 = AF2 + FC2
= AF2 + (DC − FD)2
= AF2 + DC2 + FD2 − 2DC * FD
= (AF2 + FD2) + DC2 − 2DC * FD
AC2 = AD2 + DC2 − 2DC * FD ……….… (iii)
Since ABCD is a parallelogram,
AB = CD … (iv)
And, BC = AD … (v)
In ΔDEA and ΔADF,
∠DEA = ∠AFD (Both 90°)
∠EAD = ∠ADF (EA || DF)
AD = AD (Common)
∴ΔEAD ≡ΔFDA (AAS congruence criterion)
⇒ EA = DF ………… (vi)
Adding equations (i) and (iii), we obtain
DA2 + AB2 + 2EA * AB + AD2 + DC2 − 2DC * FD = DB2 + AC2
DA2 + AB2 + AD2 + DC2 + 2EA * AB − 2DC * FD = DB2 + AC2
BC2 + AB2 + AD2 + DC2 + 2EA * AB − 2AB * EA = DB2 + AC2
[Using equations (iv) and (vi)]
AB2 + BC2 + CD2 + DA2 = AC2 + BD2
Question : 7:In Fig. 6.61, two chords AB and CD intersect each other at the point P.
Prove that: (i) Δ APC ~ Δ DPB (ii) AP . PB = CP . DP
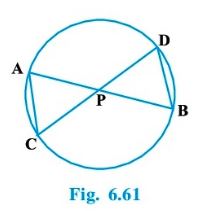
Answer :
Join CB as shown in the figure.
(i) In ΔAPC and ΔDPB,
∠ APC = ∠ DPB [Vertically opposite angles]
∠ CAP = ∠ BDP [angles in the same segment]
So, Δ APC ~ Δ DPB [AAA similarity]
(ii) Since Δ APC ~ Δ DPB [Proved]
We know that the corresponding sides of similar triangles are proportional.
So, AP/DP = PC/PB = CA/BD
⇒ AP/DP = PC/PB
⇒ AP * PB = PC * DP
Question : 8:In Fig. 6.62, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) Δ PAC ~ Δ PDB
(ii) PA . PB = PC . PD
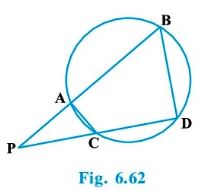
Answer :
(i) In ΔPAC and ΔPDB,
∠P = ∠P (Common)
∠PAC = ∠PDB (Exterior angle of a cyclic quadrilateral is ∠PCA = ∠PBD equal to the opposite
interior angle)
So, ΔPAC ∼ΔPDB [AA Similarity]
(ii)We know that the corresponding sides of similar triangles are proportional.
So, PA/PD = AC/DB = PC/PB
⇒ PA/PD = PC/PB
⇒ PA * PB = PC * PD
Question : 9:In Fig. 6.63, D is a point on side BC of Δ ABC such that BD/CD = AB/AC. Prove that AD is the bisector of ∠ BAC.
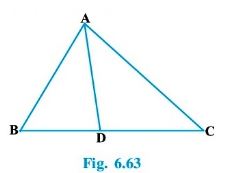
Answer :
Let us extend BA to P such that AP = AC. Join PC.
It is given that,
BD/CD = AB/AC
⇒ BD/CD = AP/AC
By using the converse of basic proportionality theorem, we obtain
AD || PC
⇒ ∠BAD = ∠APC (Corresponding angles) ……..… (1)
and, ∠DAC = ∠ACP (Alternate interior angles) ……… (2)
By construction, we have
AP = AC
⇒ ∠APC = ∠ACP ……… (3)
On comparing equations (1), (2), and (3), we obtain
∠BAD = ∠APC
⇒ AD is the bisector of the angle BAC.
Question : 10: Nazima is fly fishing in a stream.
The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of
the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string
(from the tip of her rod to the fly) is taut, how much string does she have out (see Fig. 6.64)?
If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?
Answer :
Let AB be the height of the tip of the fishing rod from the water surface. Let BC be the
horizontal distance of the fly from the tip of the fishing rod.
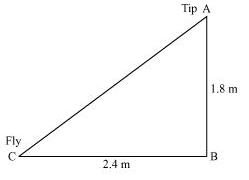
AC can be found by applying Pythagoras theorem in ΔABC.
AC2 = AB2 + BC2
⇒ AC2 = (1.8)2 + (2.4)2
⇒ AC2 = 3.24 + 5.76
⇒ AC2 = 9.00
⇒ AC = √9
⇒ AC = 3
Thus, the length of the string out is 3 m.
She pulls the string at the rate of 5 cm per second.
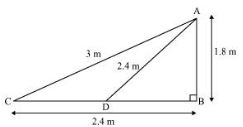
Let the fly be at point D after 12 seconds.
Length of string out after 12 seconds is AD.
AD = AC − String pulled by Nazima in 12 seconds
= (3.00 − 0.6) m
= 2.4 m
In ΔADB,
AB2 + BD2 = AD2
⇒ (1.8) 2 + BD2 = (2.4) 2
⇒ BD2 = 5.76 − 3.24
⇒ BD2 = 2.52
⇒ BD = √2.52
⇒ BD = 1.587
Horizontal distance of fly = BD + 1.2 m
= (1.587 + 1.2) m
= 2.787 m
= 2.79 m


