Class 11 - Mathematics
Relation - Exercise 2.2

Top Block 1
Question 1:
Let A = {1, 2, 3,…,14}. Define a relation R from A to A by R = {(x, y): 3x – y = 0, where x, y ∈ A}.
Write down its domain, co-domain and range.
Answer:
The relation R from A to A is given as R = {(x, y): 3x – y = 0, where x, y ∈ A}
i.e., R = {(x, y): 3x = y, where x, y ∈ A}
So, R = {(1, 3), (2, 6), (3, 9), (4, 12)}
The domain of R is the set of all first elements of the ordered pairs in the relation.
So, Domain of R = {1, 2, 3, 4}
The whole set A is the co-domain of the relation R.
So, Co-domain of R = A = {1, 2, 3… 14}
The range of R is the set of all second elements of the ordered pairs in the relation.
Hence, Range of R = {3, 6, 9, 12}
Question 2:
Define a relation R on the set N of natural numbers by R = {(x, y): y = x + 5, x is a natural number less than 4; x, y ∈N}.
Depict this relationship using roster form. Write down the domain and the range.
Answer:
R = {(x, y): y = x + 5, x is a natural number less than 4, x, y ∈ N}
The natural numbers less than 4 are 1, 2, and 3.
So, R = {(1, 6), (2, 7), (3, 8)}
The domain of R is the set of all first elements of the ordered pairs in the relation.
So, Domain of R = {1, 2, 3}
The range of R is the set of all second elements of the ordered pairs in the relation.
Hence, Range of R = {6, 7, 8}
Question 3:
A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y): the difference between x and y is odd; x ∈ A, y ∈ B}.
Write R in roster form.
Answer:
Given, A = {1, 2, 3, 5} and B = {4, 6, 9}
R = {(x, y): the difference between x and y is odd; x ∈ A, y ∈ B}
Hence, R = {(1, 4), (1, 6), (2, 9), (3, 4), (3, 6), (5, 4), (5, 6)}
Question 4:
The Fig2.7 shows a relationship between the sets P and Q.
Write this relation
(i) in set-builder form
(ii) roster form.
What is its domain and range?
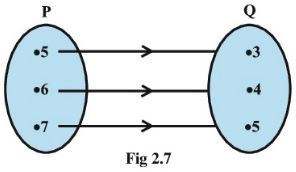
Answer:
According to the given figure, P = {5, 6, 7}, Q = {3, 4, 5}
(i) R = {(x, y): y = x – 2; x ∈ P} or R = {(x, y): y = x – 2 for x = 5, 6, 7}
(ii) R = {(5, 3), (6, 4), (7, 5)}
Now, Domain of R = {5, 6, 7}
and Range of R = {3, 4, 5}
Mddle block 1
Question 5:
Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by
{(a, b): a , b ∈A, b is exactly divisible by a}.
(i) Write R in roster form
(ii) Find the domain of R
(iii) Find the range of R.
Answer:
Given, A = {1, 2, 3, 4, 6}, R = {(a, b): a, b ∈ A, b is exactly divisible by a}
(i) R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}
(ii) Domain of R = {1, 2, 3, 4, 6}
(iii) Range of R = {1, 2, 3, 4, 6}
Question 6:
Determine the domain and range of the relation R defined by
R = {(x, x + 5): x ∈ {0, 1, 2, 3, 4, 5}}.
Answer:
Given, R = {(x, x + 5): x ∈ {0, 1, 2, 3, 4, 5}}
So, R = {(0, 5), (1, 6), (2, 7), (3, 8), (4, 9), (5, 10)}
Now, Domain of R = {0, 1, 2, 3, 4, 5}
and Range of R = {5, 6, 7, 8, 9, 10}
Question 7:
Write the relation R = {(x, x3): x is a prime number less than 10} in roster form.
Answer:
Given, R = {(x, x3): x is a prime number less than 10}
The prime numbers less than 10 are 2, 3, 5, and 7.
So, R = {(2, 8), (3, 27), (5, 125), (7, 343)}
Question 8:
Let A = {x, y, z} and B = {1, 2}. Find the number of relations from A to B.
Answer:
It is given that A = {x, y, z} and B = {1, 2}.
Now, A * B = {(x, 1), (x, 2), (y, 1), (y, 2), (z, 1), (z, 2)}
Since n(A * B) = 6, the number of subsets of A * B is 26.
Therefore, the number of relations from A to B is 26.
Question 9:
Let R be the relation on Z defined by R = {(a, b): a, b ∈ Z, a – b is an integer}. Find the domain and range of R.
Answer:
R = {(a, b): a, b ∈ Z, a – b is an integer}
It is known that the difference between any two integers is always an integer.
So, Domain of R = Z
and Range of R = Z
Bottom Block 3
Click here to visit Official CBSE website
Click here for NCERT solutions
Click here to visit Official Website of NCERT
Click here to download NCERT Textbooks

