Class 11 - Mathematics
Straight Lines - Exercise 10.1

Top Block 1
Question 1:
Draw a quadrilateral in the Cartesian plane, whose vertices are (–4, 5), (0, 7), (5, –5) and (-4,-2). Also, find its area.
Answer:
Let ABCD be the given quadrilateral with vertices A (–4, 5), B (0, 7), C (5, –5) and D (-4, -2).
Then, by plotting A, B, C, and D on the Cartesian plane and joining AB, BC, CD, and DA, the
given quadrilateral can be drawn as
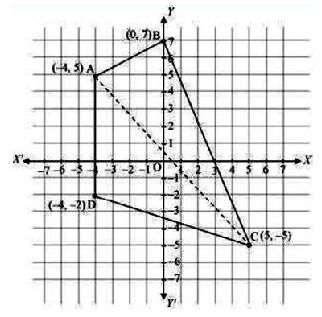
Accordingly, area (ABCD) = area (∆ABC) + area (∆ACD)
We know that the area of a triangle whose vertices are (x1, y1), (x2, y2), and (x3, y3) is
(1/2)|x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)|
Therefore, area of ∆ABC = (1/2)|-4(7 + 5) + 0(-5 – 5) + 5(5 – 7)|
= (1/2)|-4 * 12 – 5 * 2|
= (1/2)|-48 – 10|
= (1/2)|-58|
= 58/2
= 20 unit2
Area of ∆ACD = (1/2)|-4(-5 + 2) + 5(-2 – 5) + (-4)(5 + 5)|
= (1/2)|4 * 3 – 5 * 7 – 4 * 10|
= (1/2)|12 -35 – 40|
= (1/2)|-63|
= 63/2 unit2
Thus, area(ABCD) = 29 + 63/2 = 121/2 unit2
Question 2:
The base of an equilateral triangle with side 2a lies along they y-axis such that the mid-point of the base is at the origin.
Find vertices of the triangle.
Answer:
Let ABC be the given equilateral triangle with side 2a.

Mddle block 1
Assume that base BC lies along the y-axis such that the mid-point of BC is at the origin.
i.e., BO = OC = a, where O is the origin.
Now, it is clear that the coordinates of point C are (0, a), while the coordinates of point B are
(0, –a).
It is known that the line joining a vertex of an equilateral triangle with the mid-point of its
opposite side is perpendicular.
Hence, vertex A lies on the y-axis.
On applying Pythagoras theorem to ∆AOC, we obtain
(AC)2 = (OA)2 + (OC)2
=> (2a)2 = (OA)2 + a2
=> 4a2 – a2 = (OA)2
=> (OA)2 = 3a2
=> OA = ±a√3
So, the coordinates of point A = (±a√3, 0)
Thus, the vertices of the given equilateral triangle are (0, a), (0, –a), and (a√3, 0) or (0, a),
(0, -a), and (-a√3, 0).
Question 3:
Find the distance between P(x1, y1) and Q(x2, y2) when:
(i) PQ is parallel to the y-axis, (ii) PQ is parallel to the x-axis.
Answer:
The given points are P(x1, y1) and Q(x2, y2).
(i) When PQ is parallel to the y-axis, x1 = x2
In this case, distance between P and Q = √{(x1 – x1)2 + (y2 – y1)2}
= √{(y2 – y1)2}
= |y2 – y1|
(ii)When PQ is parallel to the x-axis, y1 = y2
In this case, distance between P and Q = √{(x2 – x1)2 + (y1 – y1)2}
= √{(x2 – x1)2}
= |x2 – x1|
Question 4:
Find a point on the x-axis, which is equidistant from the points (7, 6) and (3, 4).
Answer:
Let (a, 0) be the point on the x axis that is equidistant from the points (7, 6) and (3, 4).
Now, √{(7 – a)2 + (6 – 0)2} = √{(3 – a)2 + (4 – 0)2}
=> √(49 + a2 – 14a + 36) = √(9 + a2 – 6a + 16)
=> √(a2 – 14a + 85) = √(a2 – 6a + 25)
On squaring both sides, we obtain
=> a2 – 14a + 85 = a2 – 6a + 25
=> -14a + 6a = 25 – 85
=> -8a = -60
=> a = 60/8 => a = 15/2
Thus, the required point on the x-axis is (15/2, 0)
Question 5:
Find the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points P (0, –4) and B (8, 0).
Answer:
The coordinates of the mid-point of the line segment joining the points P (0, –4) and B (8, 0)
are {(0 + 8)/2, (-4 + 0)/2} = (4, -2)
It is known that the slope (m) of a non-vertical line passing through the points (x1, y1) and
(x2, y2) is given by m = (y2 – y1)/(x2 – x1), x2 ≠ x1
Therefore, the slope of the line passing through (0, 0) and (4, –2) is
(-2 – 0)/(4 – 0) = -2/4 = -1/2
Hence, the required slope of the line is -1/2
Question 6:
Without using the Pythagoras theorem, show that the points (4, 4), (3, 5) and (–1, –1) are the vertices of a right angled triangle.
Answer:
The vertices of the given triangle are A (4, 4), B (3, 5), and C (–1, –1).
It is known that the slope (m) of a non-vertical line passing through the points (x1, y1) and
(x2, y2) is given by m = (y2 – y1)/(x2 – x1), x2 ≠ x1
Slope of AB (m1) = (5 – 4)/(3 – 4) = -1
Slope of BC (m2) = (-1 – 5)/(-1 – 3) = -6/-4 = 3/2
Slope of CA (m3) = (4 + 1)/(4 + 1) = 5/5 = 1
It is observed that m1 * m3 = –1
This shows that line segments AB and CA are perpendicular to each other i.e., the given
triangle is right-angled at A (4, 4).
Thus, the points (4, 4), (3, 5), and (–1, –1) are the vertices of a right-angled triangle.
Question 7:
Find the slope of the line, which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.
Answer:
If a line makes an angle of 30° with the positive direction of the y-axis measured anticlockwise,
then the angle made by the line with the positive direction of the x-axis measured
anti –clockwise is 90° + 30° = 120°.
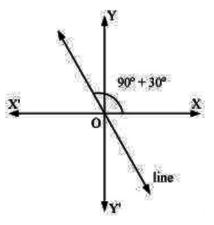
tan 120° = tan(180° – 60°) = –tan 60° = -√3
Question 8:
Find the value of x for which the points (x, –1), (2, 1) and (4, 5) are collinear.
Answer:
If points A (x, –1), B (2, 1), and C (4, 5) are collinear, then
Slope of AB = Slope of BC
=> {1 – (-1)}/(2 – x) = (5 – 1)/(4 – 2)
=> (1 + 1)/(2 – x) = 4/2
=> 2/(2 – x) = 2
=> 2 = 2(2 – x)
=> 2 = 4 – 2x
=> 2x = 4 – 2
=> 2x = 2
=> x = 1
Thus, the required value of x is 1
Question 9:
Without using distance formula, show that points (–2, –1), (4, 0), (3, 3) and (–3, 2) are vertices of a parallelogram.
Answer:
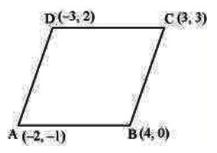
Slope of AB = (0 + 1)/(4 + 2) = 1/6
Slope of CD = (2 – 3)/(-3 – 3) = -1/-6 = 1/6
So, Slope of AB = Slope of CD
=> AB and CD are parallel to each other.
Now, slope of BC = (3 – 0)/(3 – 4) = 3/(-1) = -3
Slope of AD = (2 + 1)/(-3 + 2) = 3/(-1) = -3
=> Slope of BC = Slope of AD
=> BC and AD are parallel to each other.
Therefore, both pairs of opposite sides of quadrilateral ABCD are parallel. Hence, ABCD is a
parallelogram.
Thus, the points (–2, –1), (4, 0), (3, 3), and (–3, 2) are the vertices of a parallelogram.
Question 10:
Find the angle between the x-axis and the line joining the points (3, –1) and (4, –2).
Answer:
The slope of the line joining the points (3, –1) and (4, –2) is
m = {-2 – (-1)}/(4 – 3) = -2 + 1 = -1
Now, the inclination (θ) of the line joining the points (3, –1) and (4, – 2) is given by
tan θ = –1
=> tan θ = tan 135°
⇒θ = 135°
Thus, the angle between the x-axis and the line joining the points (3, –1) and (4, –2) is 135°.
Question 11:
The slope of a line is double of the slope of another line. If tangent of the angle between them is 1/3, find the slopes of the lines.
Answer:
Let m1 and m be the slopes of the two given lines such that m1 = 2m.
We know that if θ is the angle between the lines l1 and l2 with slopes m1 and m2, then
tan θ = |(m2 – m1)/(1 + m1 m2)|
It is given that the tangent of the angle between the two lines is 1/3
=> 1/3 = |(m – 2m)/(1 + 2m * m)|
=> 1/3 = |-m/(1 + 2m2)|
=> 1/3 = -m/(1 + 2m2) or 1/3 = -{-m/(1 + 2m2)}
Case I:
1/3 = -m/(1 + 2m2)
=> 1 + 2m2 = -3m
=> 2m2 + 3m + 1 = 0
=> (m + 1)(2m + 1) = 0
=> m = -1, -1/2
If m = –1, then the slopes of the lines are –1 and –2
If m = -1/2, then the slopes of the lines are -1/2 and –1
Case II:
1/3 = -{-m/(1 + 2m2)}
=> 1/3 = m/(1 + 2m2)
=> 1 + 2m2 = 3m
=> 2m2 – 3m + 1 = 0
=> (m – 1)(2m – 1) = 0
=> m = 1, 1/2
If m = 1, then the slopes of the lines are 1 and 2.
If m = 1/2, then the slopes of the lines are 1/2 and 1
Hence, the slopes of the lines are –1 and –2 or -1/2 and –1 or 1 and 2 or 1/2 and 1
Question 12:
A line passes through (x1, y1) and (h, k). If slope of the line is m, show that k – y1 = m(h – x1).
Answer:
The slope of the line passing through (x1, y1) and (h, k) is (k – y1)/(h – x1)
It is given that the slope of the line is m.
=> m = (k – y1)/(h – x1)
=> k – y1 = m(h – x1)
Hence, k – y1 = m(h – x1)
Question 13:
If three point (h, 0), (a, b) and (0, k) lie on a line, show that a/h + b/k = 1
Answer:
If the points A (h, 0), B (a, b), and C (0, k) lie on a line, then
Slope of AB = Slope of BC
=> (b – 0)/(a – h) = (k – b)/(0 – a)
=> b/(a – h) = (k – b)/(-a)
=> -ab = (k – b)(a – h)
=> -ab = ka – kh – ab + bh
=> ka + bh = kh
On dividing both sides by kh, we get
=> ka/kh + bh/kh = kh/kh
=> a/h + b/k = 1
Hence, a/h + b/k = 1
Question 14:
Consider the given population and year graph. Find the slope of the line AB and using it, find what will be the population in the year 2010?
Answer:

(97 – 92)/(1995 – 1985) = 5/10 = 1/2
Let y be the population in the year 2010. Then, according to the given graph, line AB must pass
through point C (2010, y).
So, Slope of AB = Slope of BC
=> 1/2 = (y – 97)/(2010 – 1995)
=> 1/2 = (y – 97)/15
=> 15/2 = y – 97
=> y – 97 = 7.5
=> y = 97 + 7.5
=> y = 104.5
Thus, the slope of line AB is 1/2 while in the year 2010, the population will be 104.5 crores.
Bottom Block 3
Click here to visit Official CBSE website
Click here for NCERT solutions
Click here to visit Official Website of NCERT
Click here to download NCERT Textbooks

