Class 10 - Mathematics
Constructions - Exercise 11.1

Top Block 1
Exercise 11.1
Question : 1:Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts. Give the justification of the construction.
Answer :
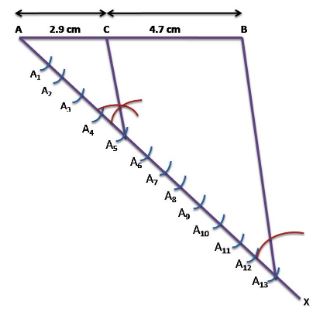
Step 1. Draw line segment AB of 7.6 cm and draw a ray AX making an acute angle with line segment AB.
Step 2. Locate 13 (= 5 + 8) points, A1, A2, A3, A4 ,…….., A13 on AX such that AA1 = A1 A2 = A2 A3 and so on.
Step 3. Join BA13.
Step 4. Through the point A5, draw a line parallel to BA13 (by making an angle equal to ∠AA13 B) at A5 intersecting AB at point C.
Now, C is the point dividing line segment AB of 7.6 cm in the required ratio of 5 : 8.
The lengths of AC and CB can be measured. It comes out to 2.9 cm and 4.7 cm respectively.
Justification:The construction can be justified by proving that
AC/CB = 5/8
By construction, we have A5 C || A13 B. By applying Basic proportionality theorem for the triangle AA13 B, we obtain
AC/BC = AA5 /A5 A13 …………… (1)
From the figure, it can be observed that AA5 and A5A13 contain 5 and 8 equal divisions of line segments respectively.
AA5 /A5 A13 = 5/8 …………. (2)
On comparing equations (1) and (2), we obtain
AC/CB = 5/8
This justifies the construction.
Question : 2:Construct a triangle of sides 4 cm, 5cm and 6cm and then a triangle similar to it whose sides are 2/3 of the corresponding sides of the first triangle.
Give the justification of the construction.
Answer :
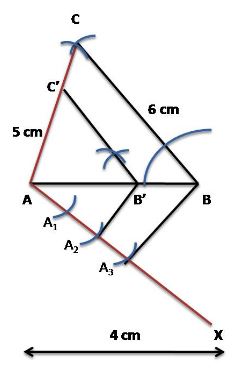
Step 1. Draw a line segment AB = 4 cm. Taking point A as centre, draw an arc of 5 cm radius.
Similarly, taking point B as its centre, draw an arc of 6 cm radius. These arcs will intersect each
other at point C. Now, AC = 5 cm and BC = 6 cm and ∆ABC is the required triangle.
Step 2. Draw a ray AX making an acute angle with line AB on the opposite side of vertex C.
Step 3. Locate 3 points A1, A2, A3 (as 3 is greater between 2 and 3) on line AX such that
A A1 = AA2 = AA3
Step 4. Join BA3 and draw a line through A2 parallel to BA3 to intersect AB at point B’.
Step 5. Draw a line through B’ parallel to the line BC to intersect AC at C’.
Now, ∆AB’C’ is the required triangle.
Justification:The construction can be justified by proving that
Mddle block 1
By construction, we have B’C’ || BC
So, ∠A = ∠ABC (Corresponding angles)
In ∆AB’C’ and ∆ABC,
∠ AB’C’ = ∠ABC (Proved above)
∠ B’AC’ = ∠BAC (Common)
So, ∆ AB’C’ ∼∆ABC (AA similarity criterion)
⇒ AB’/AB = BC’/BC = AC’/AC ………..1
In ∆AA2 B’ and ∆AA3 B,
∠A2 AB’ = ∠A3 AB (Common)
∠AA2 B’ = ∠AA3 B (Corresponding angles)
So, ∆AA2 B’ ∼∆AA3 B (AA similarity criterion)
⇒ AB’/AB = AA2/AA3
⇒ AB’/AB = 2/3 ………..2
From equations 1 and 2, we obtain
AB’/AB = B’C’/BC = AC’/AC = 2/3
⇒ AB’ = 2AB/3, B’C’ = 2BC/3, AC’ = 2AC/3
This justifies the construction.
Question : 3:Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are 7/5 of the corresponding sides of the first triangle.
Give the justification of the construction.
Answer :
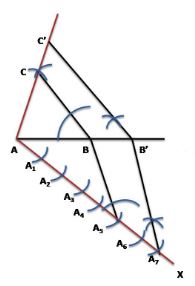
radius respectively. Let these arcs intersect each other at point C. ∆ABC is the required triangle
having length of sides as 5 cm, 6 cm, and 7 cm respectively.
Step 2. Draw a ray AX making acute angle with line AB on the opposite side of vertex C.
Step 3. Locate 7 points, A1, A2, A3, A4 , A5, A6, A7 (as 7 is greater between 5and 7), on
line AX such that AA1 = A1 A2 = A2 A3 = A3 A4 = A4 A5 = A5 A6 = A6 A7.
Step 4. Join B5 and draw a line through A7 parallel to BA5 to intersect extended line segment AB
at point B’.
Step 5. Draw a line through B’ parallel to BC intersecting the extended line segment AC at C’.
Now, ∆AB’C’ is the required triangle.
Justification:The construction can be justified by proving that
AB’ = 7AB/5, B’C’ = 7BC/5, AC’ = 7AC/5
In ∆ABC and ∆AB’C’,
∠ABC = ∠AB’C’ (Corresponding angles)
∠BAC = ∠B’AC’ (Common)
So, ∆ABC ∼∆AB’C’ (AA similarity criterion)
⇒ AB/AB’ = BC/B’C’ = AC/AC’ ………. (1)
In ∆AA5 B and ∆AA7 B’,
∠A5 AB = ∠A7 AB’ (Common)
∠AA5 B = ∠AA7 B’ (Corresponding angles)
So, ∆AA5 B ∼∆AA7 B’ (AA similarity criterion)
⇒ AB/AB’ = AA5 /AA7
⇒ AB/AB’ = 5/7 ………….(2)
On comparing equations (1) and (2), we obtain
AB/AB’ = BC/B’C’ = AC/AC’ = 5/7
AB’ = 7AB/5, B’C’ = 7BC/5, AC’ = 7AC/5
This justifies the construction.
Question : 4:Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose side are
1½ times the corresponding sides of the isosceles triangle. Give the justification of the construction.
Answer :
Let us assume that ∆ABC is an isosceles triangle having CA and CB of equal lengths, base AB of
8 cm, and AD is the altitude of 4 cm.
The ∆AB’C’ whose sides are 3/2 times of ∆ABC can be drawn as follows:
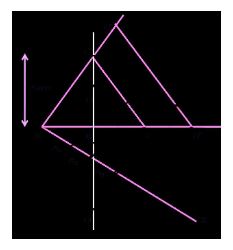
segment while taking point A and B as its centre. Let these arcs intersect each other at O and
O’. Join OO’. Let OO’ intersect AB at D.
Step 2. Taking D as centre, draw an arc of 4 cm radius which cuts the extended line segment
OO’ at point C. An isosceles ∆ABC is formed, having CD (altitude) as 4 cm and AB (base) as 8
cm.
Step 3. Draw a ray AX making an acute angle with line segment AB on the opposite side of
vertex C.
Step 4. Locate 3 points (as 3 is greater between 3 and 2) A1, A2, and A3 on AX such that
AA1 = A1 A2 = A2 A3.
Step 5. Join BA2 and draw a line through A3 parallel to BA2 to intersect extended line segment
AB at point B’.
Step 6. Draw a line through B’ parallel to BC intersecting the extended line segment AC at C’.
Now, ∆AB’C’ is the required triangle.
Justification:The construction can be justified by proving that
AB’ = 3AB/2, B’C’ = 3BC/2, AC’ = 3AC/2
In ∆ABC and ∆AB’C’,
∠ABC = ∠AB’C’ (Corresponding angles)
∠BAC = ∠B’AC’ (Common)
So, ∆ABC ∼∆AB’C’ (AA similarity criterion)
⇒ AB/AB’ = BC/B’C’= AC/AC’ …….. (1)
In ∆AA2 B and ∆AA3 B’,
∠A2 AB = ∠A3 AB’ (Common)
∠AA2 B = ∠AA3 B’ (Corresponding angles)
So, ∆AA2 B ∼∆AA3 B’ (AA similarity criterion)
⇒ AB/AB’ = AA2 /AA3
⇒ AB/AB’ = 2/3 ………..(2)
On comparing equations (1) and (2), we obtain
AB/AB’ = BC/B’C’ = AC/AC’ = 2/3
AB’ = 3AB/2, B’C’ = 3BC/2, AC’ = 3AC/2
This justifies the construction.
Question : 5:Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°.
Then construct a triangle whose sides are 3/4 of the corresponding sides of the triangle ABC. Give the justification of the construction.
Answer :
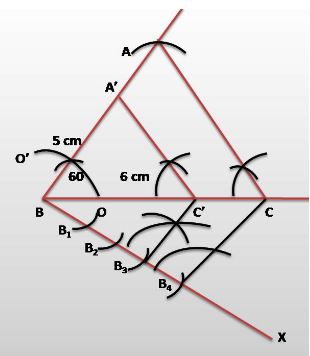
Step 1. Draw a ∆ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°.
Step 2. Draw a ray BX making an acute angle with BC on the opposite side of vertex A.
Step 3. Locate 4 points (as 4 is greater in 3 and 4), B1, B2, B3, B4, on line segment BX.
Step 4. Join B4 C and draw a line through B3, parallel to B4C intersecting BC at C’.
Step 5. Draw a line through C’ parallel to AC intersecting AB at A’. ∆A’BC’ is the required
triangle.
Justification:The construction can be justified by proving
A’B = 3AB/4, BC’ = 3BC/4, A’C’ = 3AC/4
In ∆A’BC’ and ∆ABC,
∠A’C’B = ∠ACB (Corresponding angles)
∠A’BC’ = ∠ABC (Common)
So, ∆A’BC’ ∼∆ABC (AA similarity criterion)
A’B/AB = BC’/BC = A’C’/AC ………. (1)
In ∆BB3 C’ and ∆BB4 C,
∠B3 BC’ = ∠B4 BC (Common)
∠BB3 C’ = ∠BB4 C (Corresponding angles)
So, ∆BB3 C’ ∼∆BB4 C (AA similarity criterion)
BC’/BC = BB3/AA4
⇒ BC’/BC = 3/4 ………….(2)
From equations (1) and (2), we obtain
⇒ A’B/AB = BC’/BC = A’C’/AC = 3/4
⇒ A’B = 3AB/4, BC’ = 3BC/4, A’C’ = 3AC/4
This justifies the construction.
Question : 6:Draw a triangle ABC with side BC = 7 cm, ∠B = 45o, ∠A = 105o. Then, construct a triangle whose sides are 4/3 times the corresponding side of ∆ABC.
Give the justification of the construction.
Answer :
Given, ∠B = 45o, ∠A = 105o
Sum of all interior angles in a triangle is 180o.
∠A + ∠B + ∠C = 180o
⇒ 105o + 45o + ∠C = 180o
⇒ ∠C = 180o− 150o
⇒ ∠C = 30o
The required triangle can be drawn as follows:

Step 2. Draw a ray BX making an acute angle with BC on the opposite side of vertex A.
Step 3. Locate 4 points (as 4 is greater in 4 and 3), B1, B2, B3, B4, on BX.
Step 4. Join B3 C. Draw a line through B4 parallel to B3 C intersecting extended BC at C’.
Step 5. Through C’, draw a line parallel to AC intersecting extended line segment at C’.
Now, ∆A’BC’ is the required triangle.
Justification:The construction can be justified by proving that
A’B = 4AB/3, BC’ = 4BC/3, A’C’ = 4AC/3
In ∆ABC and ∆A’BC’,
∠ABC = ∠A’BC’ (Common)
∠ACB = ∠A’C’B (Corresponding angles)
So, ∆ABC ∼∆A’BC’ (AA similarity criterion)
AB/A’B = BC/BC’ = AC/A’C’ ……… (1)
In ∆BB3 C and ∆BB4 C’,
∠B3 BC = ∠B4 BC’ (Common)
∠BB3 C = ∠BB4 C’ (Corresponding angles)
So, ∆BB3 C ∼∆BB4 C’ (AA similarity criterion)
BC/BC’ = BB3 /BB4
⇒ BC/BC’ = 3/4 ………….(2)
On comparing equations (1) and (2), we obtain
⇒ AB/A’B = BC/BC’ = AC/A’C’ = 3/4
⇒ A’B = 4AB/3, BC’ = 4BC/3, A’C’ = 4AC/3
This justifies the construction.
Question : 7:Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm.
the construct another triangle whose sides are 5/3 times the corresponding sides of the given triangle. Give the justification of the construction.
Answer :
It is given that sides other than hypotenuse are of lengths 4 cm and 3 cm. Clearly, these will be
perpendicular to each other. The required triangle can be drawn as follows:
Step 1. Draw a line segment AB = 4 cm. Draw a ray SA making 90o with it.
Step 2. Draw an arc of 3 cm radius while taking A as its centre to intersect SA at C. Join BC.
So, ∆ABC is the required triangle.
Step 3. Draw a ray AX making an acute angle with AB, opposite to vertex C.
Step 4. Locate 5 points (as 5 is greater in 5 and 3), A1, A2, A3, A4, A5, on line segment AX such
that AA1 = A1 A2 = A2 A3 = A3 A4 = A4 A5.
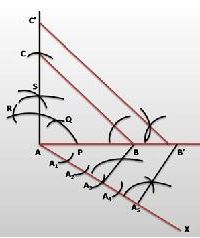
Step 6. Through B’, draw a line parallel to BC intersecting extended line segment AC at C’.
So, ∆AB’C’ is the required triangle.
Justification:The construction can be justified by proving that
AB’ = 5AB/3, B’C’ = 5BC/3, AC’ = 5AC/3
In ∆ABC and ∆AB’C’,
∠ABC = ∠AB’C’ (Corresponding angles)
∠BAC = ∠B’AC’ (Common)
So, ∆ABC ∼∆AB’C’ (AA similarity criterion)
AB/AB’ = BC/B’C’ = AC/AC’ …………. (1)
In ∆AA3 B and ∆AA5 B’,
∠A3 AB = ∠A5 AB’ (Common)
∠AA3 B = ∠AA5 B’ (Corresponding angles)
So, ∆AA3 B ∼∆AA5 B’ (AA similarity criterion)
⇒ AB/AB’ = AA3 /AA5
⇒ AB/AB’ = 3/5 ………..(2)
On comparing equations (1) and (2), we obtain
AB/AB’ = BC/B’C’ = AC/AC’ = 3/5
AB’ = 5AB/3, B’C’ = 5BC/3, AC’ = 5AC/3
This justifies the construction.

