Class 10 - Mathematics
Constructions - Exercise 11.2

Top Block 1
Exercise 11.2
Question : 1:Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Give the justification of the construction.
Answer :
A pair of tangents to the given circle can be constructed as follows:
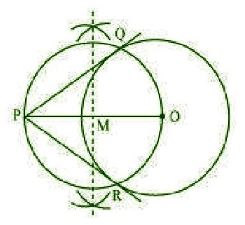
point P, 10 cm away from O. Join OP.
Step 2. Bisect OP. Let M be the mid-point of PO.
Step 3. Taking M as centre and MO as radius, draw a circle.
Step 4. Let this circle intersect the previous circle at point Q and R.
Step 5. Join PQ and PR. PQ and PR are the required tangents.
The lengths of tangents PQ and PR are 8 cm each.
Justification:
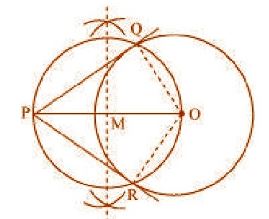
Mddle block 1
(whose centre is O and radius is 6 cm). For this, join OQ and OR.
∠PQO is an angle in the semi-circle. We know that angle in a semi-circle is a right angle.
So, ∠PQO = 90o
⇒ OQ ⊥ PQ
Since OQ is the radius of the circle, PQ has to be a tangent of the circle.
Similarly, PR is a tangent of the circle.
Question : 2:Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length.
Also verify the measurement by actual calculation. Give the justification of the construction.
Answer :
Tangents on the given circle can be drawn as follows:
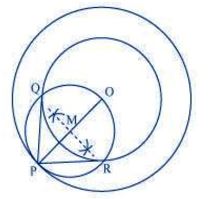
Step 2. Draw a circle of 6 cm radius taking O as its centre. Locate a point P on this circle and
join OP.
Step 3. Bisect OP. Let M be the mid-point of PO.
Step 4. Taking M as its centre and MO as its radius, draw a circle. Let it intersect the given
circle at the points Q and R.
Step 5. Join PQ and PR. PQ and PR are the required tangents.
It can be observed that PQ and PR are of length 4.47 cm each.
In ∆PQO,
Since PQ is a tangent,
∠PQO = 90o
PO = 6 cm
QO = 4 cm
Applying Pythagoras theorem in ∆PQO, we obtain
PQ2 + QO2 = PQ2
⇒ PQ2 + 42 = 62
⇒ PQ2 + 16 = 36
⇒ PQ2 = 36 − 16
⇒ PQ2 = 20
⇒ PQ = √20
⇒ PQ = 4.47 cm
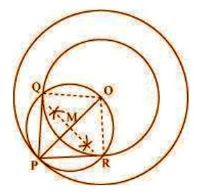
(whose centre is O and radius is 4 cm). For this, let us join OQ and OR.
∠PQO is an angle in the semi-circle. We know that angle in a semi-circle is a right angle.
So, ∠PQO = 90o
⇒ OQ ⊥ PQ
Since OQ is the radius of the circle, PQ has to be a tangent of the circle.
Similarly, PR is a tangent of the circle.
Question : 3:Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre.
Draw tangents to the circle from these two points P and Q. Give the justification of the construction.
Answer :
The tangent can be constructed on the given circle as follows:
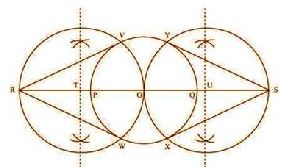
Step 2. Take one of its diameters, PQ, and extend it on both sides. Locate two points on this
diameter such that OR = OS = 7 cm.
Step 3. Bisect OR and OS. Let T and U be the mid-points of OR and OS respectively.
Step 4. Taking T and U as its centre and with TO and UO as radius, draw two circles. These two
circles will intersect the circle at point V, W, X, Y respectively. Join RV, RW, SX, and SY.
These are the required tangents.
Justification:
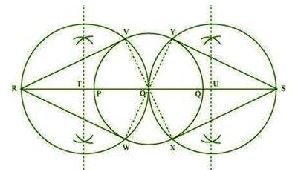
circle (whose centre is O and radius is 3 cm). For this, join OV, OW, OX, and OY.
∠RVO is an angle in the semi-circle. We know that angle in a semi-circle is a right angle.
So, ∠RVO = 90o
⇒ OV ⊥ RV
Since OV is the radius of the circle, RV has to be a tangent of the circle.
Similarly, OW, OX, and OY are the tangents of the circle.
Question : 4:Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60o. Give the justification of the construction.
Answer :
The tangents can be constructed in the following manner:
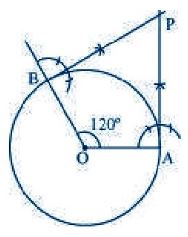
Step 2. Take a point A on the circumference of the circle and join OA. Draw a perpendicular to
OA at point A.
Step 3. Draw a radius OB, making an angle of 120o (180o − 60o) with OA.
Step 4. Draw a perpendicular to OB at point B. Let both the perpendiculars intersect at point P.
PA and PB are the required tangents at an angle of 60o.
Justification:The construction can be justified by proving that ∠APB = 60o
By our construction
∠OAP = 90o
∠OBP = 90o
and ∠AOB = 120o
We know that the sum of all interior angles of a quadrilateral = 360o
∠OAP + ∠AOB + ∠OBP + ∠APB = 360o
⇒ 90o + 120o + 90o + ∠APB = 360o
⇒ 300o + ∠APB = 360o
⇒ ∠APB = 360o – 300o
⇒ ∠APB = 60o
This justifies the construction.
Question : 5:Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre,
draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle. Give the justification of the construction.
Answer :
The tangents can be constructed on the given circles as follows:
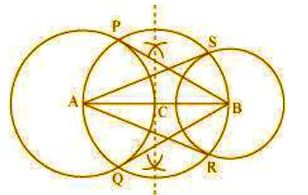
3 cm radius.
Step 2. Bisect the line AB. Let the mid-point of AB be C. Taking C as centre, draw a circle of AC
radius which will intersect the circles at points P, Q, R, and S. Join BP, BQ, AS, and AR.
These are the required tangents.
Justification:
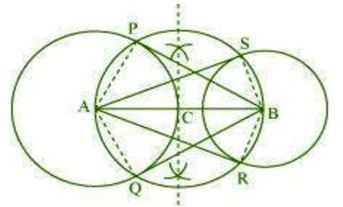
(whose centre is B and radius is 3 cm) and BP and BQ are the tangents of the circle (whose
centre is A and radius is 4 cm). For this, join AP, AQ, BS, and BR.
∠ASB is an angle in the semi-circle. We know that an angle in a semi-circle is a right angle.
So, ∠ASB = 90o
⇒ BS ⊥ AS
Since BS is the radius of the circle, AS has to be a tangent of the circle.
Similarly, AR, BP, and BQ are the tangents.
Question : 6:Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B = 90o. BD is the perpendicular from B on AC.
The circle through B, C, and D is drawn. Construct the tangents from A to this circle. Give the justification of the construction.
Answer :
Consider the following situation. If a circle is drawn through B, D, and C, BC will be its diameter
as ∠BDC is of measure 90o. The centre E of this circle will be the mid-point of BC.
The required tangents can be constructed on the given circle as follows:
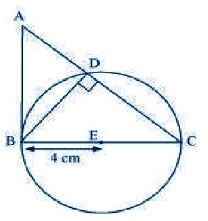
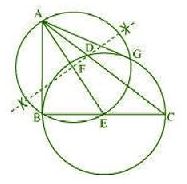
point B and G. Join AG.
AB and AG are the required tangents.
Justification:The construction can be justified by proving that AG and AB are the tangents to the circle. For
this, join EG.
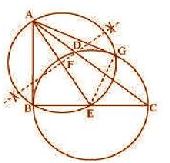
So, ∠AGE = 90o
⇒ EG ⊥ AG
Since EG is the radius of the circle, AG has to be a tangent of the circle.
Again, ∠B = 90o
⇒ AB ⊥ BE
Since BE is the radius of the circle, AB has to be a tangent of the circle.
Question : 7:Draw a circle with the help of a bangle. Take a point outside the circle.
Construct the pair of tangents from this point to the circles. Give the justification of the construction.
Answer :
The required tangents can be constructed on the given circle as follows:
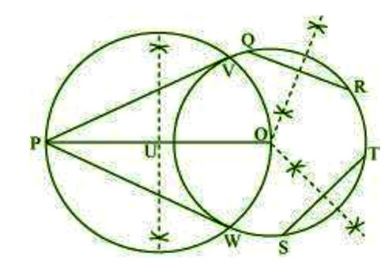
Step 2. Take a point P outside this circle and take two chords QR and ST.
Step 3. Draw perpendicular bisectors of these chords. Let them intersect each other at point O.
Step 4. Join PO and bisect it. Let U be the mid-point of PO. Taking U as centre, draw a circle of
radius OU, which will intersect the circle at V and W. Join PV and PW.
PV and PW are the required tangents.
Justification:
this, first of all, it has to be proved that O is the centre of the circle. Let us join OV and OW.
We know that perpendicular bisector of a chord passes through the centre. Therefore, the
perpendicular bisector of chords QR and ST pass through the centre. It is clear that the
intersection point of these perpendicular bisectors is the centre of the circle. ∠PVO is an angle
in the semi-circle. We know that an angle in a semi-circle is a right angle.
So, ∠PVO = 90o
⇒ OV ⊥ PV
Since OV is the radius of the circle, PV has to be a tangent of the circle.
Similarly, PW is a tangent of the circle.

