Class 11 - Mathematics
Straight Lines - Exercise 10-Misc

Top Block 1
Question 1:
Find the values of k for which the line is (k – 3)x – (4 – k2)y + k2 – 7k + 6 = 0
(a) Parallel to the x-axis, (b) Parallel to the y-axis, (c) Passing through the origin.
Answer:
The given equation of line is
(k – 3)x – (4 – k2)y + k2 – 7k + 6 = 0 ………….1
(a) If the given line is parallel to the x-axis, then
Slope of the given line = Slope of the x-axis
The given line can be written as
(4 – k2)y = (k – 3) x + k2 – 7k + 6 = 0, which is of the form y = mx + c.
Slope of the given line = (k – 3)/(4 – k2)
Slope of the x-axis = 0
So, (k – 3)/ (4 – k2) = 0
=> k – 3 = 0
=> k = 3
Thus, if the given line is parallel to the x-axis, then the value of k is 3.
(b) If the given line is parallel to the y-axis, it is vertical. Hence, its slope will be undefined.
The slope of the given line is (k – 3)/(4 – k2)
Now, (k – 3)/(4 – k2) is undefined at k2 = 4
=> k2 = 4
=> k = ±2
Thus, if the given line is parallel to the y-axis, then the value of k is ±2.
(c) If the given line is passing through the origin, then point (0, 0) satisfies the given equation
of line.
(k – 3) * 0 – (4 – k2) * 0 + k2 – 7k + 6 = 0
=> k2 – 7k + 6 = 0
=> (k – 6)(k – 1) = 0
=> k = 6, 1
Thus, if the given line is passing through the origin, then the value of k is either 1 or 6.
Question 2:
Find the values of θ and p, if the equation x cos θ + y sin θ = p is the normal form of the line √3x + y + 2 = 0.
Answer:
The equation of the given line is √3x + y + 2 = 0
This equation can be reduced as
√3x + y + 2 = 0
=> -√3x – y = 2
On dividing both sides by √{(-√3)2 + (-1)2} = 2, we obtain
=> -√3x/2 – y/2 = 2/2
=> (-√3/2)x + (-1/2)y = 1 …………..1
Comparing equation 1 to x cos θ + y sin θ = p, we get
cos θ = -√3/2, sin θ = -1/2 and p = 1
Since the values of sin θ and cos θ are negative,
So, θ = π + π/6 = 7π/6
Thus, the respective values of θ and p are 7π/6 and 1.
Question 3:
Find the equations of the lines, which cut-off intercepts on the axes whose sum and product are 1 and –6, respectively.
Answer:
Let the intercepts cut by the given lines on the axes be a and b.
It is given that
a + b = 1 ………..1
ab = –6 ………..2
On solving equations 1 and 2, we get
a = 3 and b = –2 or a = –2 and b = 3
It is known that the equation of the line whose intercepts on the axes are a and b is
x/a + y/b = 1
=> bx + ay – ab = 0
Case I: a = 3 and b = –2
In this case, the equation of the line is –2x + 3y + 6 = 0, i.e., 2x – 3y = 6
Case II: a = –2 and b = 3
In this case, the equation of the line is 3x – 2y + 6 = 0, i.e., –3x + 2y = 6
Thus, the required equation of the lines are 2x – 3y = 6 and –3x + 2y = 6
Question 4:
What are the points on the y-axis whose distance from the line x/3 + y/4 = 1 is 4 units.
Answer:
Let (0, b) be the point on the y-axis whose distance from line x/3 + y/4 = 1 is 4 units.
The given line can be written as
4x + 3y – 12 = 0 ………….1
On comparing equation (1) to the general equation of line Ax + By + C = 0, we get
A = 4, B = 3, and C = –12
It is known that the perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is
given by d = |Ax1 + By1 + C|/√(A2 + B2)
Therefore, if (0, b) is the point on the y-axis whose distance from line x/3 + y/4 = 1 is 4
units, then:
4 = |4 * 0 + 3 * b – 12|/√(42 + 32)
=> 4 = |3b – 12|/5
=> 20 = ±(3b – 120
=> 20 = 3b – 12 or 20 = -(3b – 12)
=> 3b = 32 or 3b = -20 + 12
=> b = 32/3 or b = -8/3
Thus, the required points are (0, 32/3) or (0, -8/3).
Question 5:
Find the perpendicular distance from the origin to the line joining the points (cos θ, sin θ) and (cos ф, sin ф)
Answer:
The equation of the line joining the points (cos θ, sin θ) and (cos ф, sin ф) is given by
y – sin θ = {(sin ф – sin θ)/(cos ф – cos θ)}(x – sin θ)
=> (y – sin θ) (cos ф – cos θ) = (sin ф – sin θ)(x – cos θ)
=> (cos ф – cos θ)y – sin θ(cos ф – cos θ) = x(sin ф – sin θ) – cos θ(sin ф – sin θ)
=> x(sin θ – sin ф) + y(cos ф – cos θ) + cos θ sin ф – cos θ sin θ –sin θ cos ф + sin θ cos θ = 0
=> x(sin θ – sin ф) + y(cos ф – cos θ) + sin (θ – ф) = 0
=> Ax + By + C = 0
Where A = sin θ – sin ф, B = cos ф – cos θ and C = sin (θ – ф)
It is known that the perpendicular distance (d) of a line Ax + By + C = 0 from a point (x1, y1) is
given by d = |Ax1 + By1 + C|/√(A2 + B2)
Therefore, the perpendicular distance (d) of the given line from point (x1, y1) = (0, 0) is
d = |(sin θ – sin ф) * 0 + (cos ф – cos θ) * 0 + sin (θ – ф)|
√{(sin θ – sin ф)2 + (cos ф – cos θ)2}
=> d = |sin (θ – ф)|/ √{sin2 θ + sin2 ф – 2 sin θ * sin ф + cos2 ф + cos2 θ – 2 cos ф * cos θ}
=> d = |sin (θ – ф)|/ √{sin2 θ + cos2 θ – 2 sin θ * sin ф + sin2 ф + cos2 ф – 2 cos ф * cos θ}
=> d = |sin (θ – ф)|/ √(1 – 2 sin θ * sin ф + 1 – 2 cos ф * cos θ)
=> d = |sin (θ – ф)|/ √(2 – 2 sin θ * sin ф – 2 cos ф * cos θ)
=> d = |sin (θ – ф)|/ √{2(1 – cos (ф – θ)}
=> d = |sin (θ – ф)|/ √{2(2sin2 (ф – θ)/2}
=> d = |sin (θ – ф)|/ |2sin (ф – θ)/2|
Question 6:
Find the equation of the line parallel to y-axis and drawn through the point of intersection of the lines x – 7y + 5 = 0 and 3x + y = 0.
Answer:
The equation of any line parallel to the y-axis is of the form
x = a …………….1
The two given lines are
x – 7y + 5 = 0 …………..2
3x + y = 0 …………..3
On solving equations (2) and (3), we get
X = -5/22 and y = 15/22
Therefore, (-5/22, 15/22) is the point of intersection of lines 2 and 3.
Since line x = a passes through point (-5/22, 15/22).
So, a = -5/22
Thus, the required equation of the line is x = -5/22
Question 7:
Find the equation of a line drawn perpendicular to the line x/4 + y/6 = 1 through the point, where it meets the y-axis.
Answer:
The equation of the given line is x/4 + y/6 = 1
This equation can also be written as
3x + 2y – 12 = 0
=> 2y = -3x + 12
=> y = -3x/2 + 6, which is of the form y = mx + c
Now, slope of the given line = -3/2
Slope of line perpendicular to the given line = -1/(-3/2) = 2/3
Let the given line intersect the y-axis at (0, y).
On substituting x with 0 in the equation of the given line, we get
y/6 = 1
=> y = 6
The given line intersects the y-axis at (0, 6).
The equation of the line that has a slope of 2/3 and passes through point (0, 6) is
(y – 6) = (2/3)(x – 0)
=> 3(y – 6) = 2x
=> 3y – 18 = 2x
=> 2x – 3y + 18 = 0
Thus, the required equation of the line is 2x – 3y + 18 = 0
Question 8:
Find the area of the triangle formed by the lines y – x = 0, x + y = 0 and x – k = 0.
Answer:
The equations of the given lines are
y – x = 0 …………..1
x + y = 0 …………..2
x – k = 0 …………..3
The point of intersection of lines 1 and 2 is given by
x = 0 and y = 0
The point of intersection of lines 2 and 3 is given by
x = k and y = –k
The point of intersection of lines 1 and 3 is given by
x = k and y = k
Thus, the vertices of the triangle formed by the three given lines are (0, 0), (k, –k), and (k, k).
We know that the area of a triangle whose vertices are (x1, y1), (x2, y2), and (x3, y3) is
(1/2)|x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)|
Therefore, area of the triangle formed by the three given lines
= (1/2)|0(-k – k) + k(k – 0) + k(0 + k)|
= (1/2)|k2 + k2|
= (1/2)|2k2|
= k2 square units
Question 9:
Find the value of p so that the three lines 3x + y – 2 = 0, px + 2y – 3 = 0 and 2x – y – 3 = 0 may intersect at one point.
Answer:
The equations of the given lines are
3x + y – 2 = 0 ……………1
px + 2y – 3 = 0 ………….2
2x – y – 3 = 0 ……………3
On solving equations 1 and 3, we obtain
x = 1 and y = –1
Since these three lines may intersect at one point, the point of intersection of lines 1 and 3 will
also satisfy line 2.
p (1) + 2 (–1) – 3 = 0
=> p – 2 – 3 = 0
=> p = 5
Thus, the required value of p is 5.
Question 10:
If three lines whose equations are y = m1x + c1, y = m2x + c2 and y = m3x + c3 are concurrent, then
show that m1(c2 – c3) + m2(c3 – c1) + m3(c1 – c2) = 0.
Answer:
Given equations are:
y = m1x + c1
=> m1 x – y + c1 = 0……….1
y = m2 x + c2
=> m2 x – y + c2 = 0……….2
y = m3 x + c3
=> m3 x – y + c3 = 0……….3
Now three lines are concurrent if
|m1 -1 c1|
|m2 -1 c2| = 0
|m3 -1 c3|
=> m1(-c3 + c2) – m2(-c3 + c1) + m3(-c2 + c1) = 0
=> m1(c2 – c3) + m2(c3 – c1) + m3(c1 – c2) = 0
Question 11:
Find the equation of the lines through the point (3, 2) which make an angle of 45° with the line x –2y = 3.
Answer:
Given point is (3, 2).
Equation of line is : x – 2y = 3
=> x – 3 = 2y
=> y = x/3 – 1
Let the slope of required line is m.
Again given that slope between required line and x – 2y = 3
tan 45° = |(1/2 – m)/(1 + m/2)|
=> 1 =|(1/2 – m)/(1 + m/2)|
Now,
1 = (1/2 – m)/(1 + m/2) and -1= (1/2 – m)/(1 + m/2) (since |x| = -x and x)
=> 1 + m/2 = 1/2 – m and -(1 + m/2) = (1/2 – m)
=> m + m/2 = 1/2 -1 and -1 – m/2 = 1/2 – m
=> 3m/2 = -1/2 and m – m/2 = 1+ 1/2
=> m = -1/3 and m/2 = 3/2
=> m =-1/3 and m = 3
Case 1: m = -1/3 and point is (3, 2)
y – 2 = (-1/3)(x – 3)
=> 3(y – 2) = -x + 3
=> 3y – 6 = -x + 3
=> 3y + x = 3+6
=> x + 3y = 9
Case 2: m = 3 and point is (3, 2)
y – 2 = 3(x – 3)
=> y-2 = 3x – 9
=> 3x – y = 9-2
=> 3x – y = 7
Thus, the equations of the lines are 3x – y = 7 and x + 3y = 9.
Question 12:
Find the equation of the line passing through the point of intersection of the lines 4x + 7y – 3 = 0 and 2x – 3y + 1 = 0
that has equal intercepts on the axes.
Answer:
Given equation of lines are :
4x + 7y – 3 = 0 ………….1
and 2x – 3y + 1 = 0 ………….2
Let the required equation of lines having equal intercept is
x/a + y/a = 1
=> x + y = a ……….3
After solving equation 1 and 2, we get
x = 1/13, = 5/13
So, (1/3, 5/13) is the point of intersection of the given lines.
Since the equation 3 passes through this point, So
1/13 + 5/13 = a
=> a = 6/13
Now put this value in equation 3, we get
x + y = 6/13
=> 13(x + y) = 6
=> 13x + 13y = 6
So, the equation of line is 13x + 13y = 6
Question 13:
Show that the equation of the line passing through the origin and making an angle θ
with the line y = mx + c is y/x = (m ± tan θ)/(1 ± m * tan θ)
Answer:
Let the equation of the line passing through the origin be y = m1x.
If this line makes an angle of θ with line y = mx + c, then angle θ is given by
So, tan θ = |(m1 – m)/(1 + m1m)|
=> tan θ = |(y/x – m)/(1 + ym/x)|
=> tan θ = ±{(y/x – m)/(1 + ym/x)}
=> tan θ = (y/x – m)/(1 + ym/x) or tan θ = -(y/x – m)/(1 + ym/x)
Case 1:
tan θ = (y/x – m)/(1 + ym/x)
=> tan θ(1 + ym/x) = (y/x – m)
=> tan θ + (ym/x) tan θ = y/x – m
=> m + tan θ = (y/x)(1 – m * tan θ)
=> y/x = (m + tan θ)/ (1 – m * tan θ)
Case 2:
tan θ = -(y/x – m)/(1 + ym/x)
=> tan θ(1 + ym/x) = -(y/x – m)
=> tan θ + (ym/x) tan θ = -y/x + m
=> m + tan θ = (y/x)(1 + m * tan θ)
=> y/x = (m + tan θ)/ (1 + m * tan θ)
Therefore, the required line is given by y/x = (m ± tan θ)/(1 ± m * tan θ)
Question 14:
In what ratio, the line joining (–1, 1) and (5, 7) is divided by the line x + y = 4?
Answer:
Given line is x + y = 4 ………….1
and points are: (-1, 1) and (5, 7)
Equation of line which joins the points
y – 1 = {(7 – 1)/(5 + 1)}*(x + 1)
=> y-1 = (6/6)*(x + 1)
=> y – 1 = x + 1
=> x – y + 1 + 1 = 0
=> x – y + 2 = 0 ……….2
After solving equation 1 and 2
x = 1, y = 3
So, (1, 3) is the point of intersection of these two lines.
Now let point (1, 3) divide the line joining (-1, 1) and (5, 7) in the ratio 1 : k
According to section formula,
(1, 3) = [{k(-1) + 1 * 5}/(1 + k), (k * 1 + 1 * 7)/(1 + k)]
=> (1, 3) = {(-k + 5)/(1 + k), (k + 7)/(1 + k)}
Now,
(-k + 5)/(1 + k) = 1
=> -k + 5 = 1 + k
=> 5 – 1= k + k
=> 4 = 2k
=> k = 2
Hence, the required ratio is 1 : 2
Question 15:
Find the distance of the line 4x + 7y + 5 = 0 from the point (1, 2) along the line 2x – y = 0.
Answer:

Mddle block 1
and equation of line PQ is 2x – y = 0 ………2
Solve the equations 1 and 2 for obtaining point Q.
From equation 2 put y = 2x in equation 1
4x + 7 × 2x + 5 = 0
4x + 14x + 5 = 0
18x + 5 = 0
x = -5/18 ,
Put it in equation 2, we get
y = 2x = -5/9
So, the co-ordinate of Q = {-5/18, -5/9}
Now, Length of PQ = √{(x2 – x1)² + (y2 – y1)²}
= √{(1 + 5/18)²+(2 + 5/9)²}
= √{(23/18)² + (23/9)²}
= √{23²{1/18² + 1/9²}
= 23√{1/9²(1/4 + 1)}
=23/9 √(1/4 + 1)
= 23/9 √(5/4)
= 23√5/18 unit
Question 16:
Find the direction in which a straight line must be drawn through the point (–1, 2) so that its point of intersection with the line x + y = 4
may be at a distance of 3 units from this point.
Answer:
Let the straight line is y = mx + c
This line passes through the point (-1, 2)
So, 2 = -m + c
=> c = m + 2
Now y = mx + m + 2 ………1
Given equation of line is : x + y = 4 ……….2
Solving equation 1 and 2, we get
x = (2 – m)/(m + 1) and y = (5m + 1)/(m + 1)
Now this point is at a distance of 3 unit from the point (-1, 2)
From distance formula
√[{(2 – m)/(m + 1) + 2}2 + {(5m + 2)/(m + 1) – 2}2] = 3
Squaring both side, we get
{(2 – m)/(m + 1) + 1}2 + {(5m + 2)/(m + 1) – 2}2 = 9
=> {(2 – m + m + 1)/(m + 1)}2 + {(5m + 2 – 2m – 2)/(m + 1)}2 = 9
=> 9/(m + 1)2 + 9m2/(m + 1)2 = 0
=> (1 + m2)/(m + 1)2 = 1 (divide by 9 on both side)
=> 1 + m2 = (m + 1)2
=> 1 + m2 = (m2 + 2m +1)
=> 1 + m2 = m2 + 2m + 1
=> 2m = 0
=> m = 0
Since the slope of the line is zero.
Hence, the line is parallel to x-axis.
Question 18:
Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
Answer:
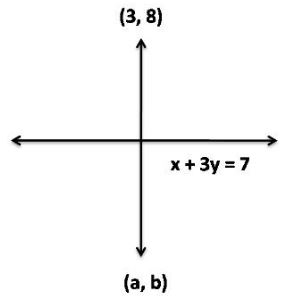
x + 3y = 7 ………1
Let the point (a, b) is the image of point (3, 8)
Slope of line AB = (b – 8)/(a – 3)
Since the given line x + 3y = 7 is perpendicular to AB
So (b – 8)/(a – 3) *(-1/3) = -1 (Since product of two slopes = -1)
=> (b – 8)/(a – 3) = 3
=> (b – 8) = 3(a – 3)
=> b – 8 = 3a – 9
=> 3a – b = 9 – 8
=> 3a – b = 1 ………2
Now mid-point of AB = {(a + 3)/3, (b + 8)/2}
This point also satisfies equation 1
So, (a + 3)/2 + 3(b + 8)/2 = 7
=> a + 3 + 3b + 24 = 2*7
=> a + 3b + 27 = 14
=> a + 3b = 14-27
=> a + 3b = -13 ……3
After solving equation 2 and 3, we get
a = -1, b = -4
Hence, the image of the point (3, 8) with respect to x + 3y = 8 is (-1,-4).
Question 19:
If the lines y = 3x + 1 and 2y = x + 3 are equally inclined to the line y = mx + 4, find the value of m.
Answer:
Given equation of line are:
y = 3x + 1 …………..1
Slope = 3
2y = x + 3
=> y = x/3 + 3/2 ………..2
Slope = 1/3
y = mx + 4 ……..3
Slope = m
Given that equation 1 and 2 are equally inclined with equation 3.
So, the angle between equation 1 and 3 = angle between equation 2 and 3
=> |(3 – m)/(1 + 3m)| = |(1/2 – m)/(1 + m/2)|
=> |(3 – m)/(1 + 3m)| = |(1 – 2m)/(2 + m)|
=> (3 – m)/(1 + 3m) = (1 – 2m)/(2 + m) and (3 – m)/(1 + 3m) = -(1 – 2m)/(2 + m)
=> (3 – m)(2 + m) = (1 – 2m)(1 + 3m) and (3 – m)*(2 + m) = -(1 + 3m)(1 – 2m)
=> 6 + 3m – 2m – m2 = 1 + 3m – 2m – 6 m2 and 6 + 3m – 2m – m2 = -(1 + 3m – 2m – 6 m2)
=> -m2 + m + 6 = 1 + m – 6m2 and -m2 + m + 6 = -1 – m + 6m2
=> 5m2 + 5 = 0 and 7m2 – 2m – 7 = 0
=> m2 + 1= 0
=> m2 = -1 which is not possible.
Again, 7m2 – 2m – 7 = 0
=> m = {2 + √(4 – 4*7*(-7))}/(2*7) and m = {2 – √(4 – 4*7*(-7))}/(2*7)
=> m = {2 + √(4 + 4*49)}/14 and m = {2 – √(4 + 4*49)}/14
=> m = {2 + 2√(1 + 49)}/14 and m = {2 – 2√(1 + 49)}/14
=> m = {1 + √50}/7 and m = {1 – √50}/7
=> m = {1 + 5√2}/7 and m = {1 – 5√2}/7
Hence, the value of m is {1 ± 5√2}/7
Question 20:
If sum of the perpendicular distances of a variable point P (x, y) from the lines x + y – 5 = 0 and 3x – 2y + 7 = 0 is always 10.
Show that P must move on a line.
Answer:
Given Point is P(x, y).
Lines are x + y – 5 = 0 and 3x – 2y + 7 =0
Now distance of P(x, y) from the line x + y – 5 = 0 is
d1 = (x + y – 5)/√(1 + 1) = (x + y – 5)/√2
Again distance of P(x, y) from the line 3x – 2y + 7 = 0 is
d2 = (3x – 2y + 7)/√{32 + (-2)2} = (3x – 2y + 7)/√(9 + 4) = (3x – 2y + 7)/√13
Given sum of distances is equal to 10
=> d1 + d2 = 10
=> (x + y – 5)/√2 + (3x – 2y + 7)/√13 = 10
=> √13*(x + y – 5) + √2*(3x – 2y + 7) = 10*√2*√13
=> x(√13 + 3√2) + y(√13 – 2√2) + (7√2 – 5√13) = 10
=> y(√13 – 2√2) = -(√13 + 3√2)x + 10 – (7√2 – 5√13)
=> y = {-(√13 + 3√2)/(√13 – 2√2)}x + {10 – (7√2 – 5√13)}/(√13 – 2√2)
This forms a line y = mx + c
Hence, the given point P(x, y) must move on a line.
Question 21:
Find equation of the line which is equidistant from parallel lines 9x + 6y – 7 = 0 and 3x + 2y + 6 = 0.
Answer:
Given equation are:
9x + 6y – 7 = 0 ………1
3x + 2y + 6 = 0………2
Now equation of line which is equidistant from both the lines is
|(9x + 6y – 7)/√(92 + 62 )| = |(3x + 2y + 6)/√(32 + 22)|
=> |(9x + 6y – 7)/√(81+36 )| = |(3x + 2y + 6)/√(9 + 4 )|
=> |(9x + 6y – 7)/√117| = |(3x + 2y + 6)/√13|
=> |(9x + 6y – 7)/√117| = |(3x + 2y + 6)/√13|
=> |(9x + 6y – 7)/√(13*9)| = |(3x + 2y + 6)/√13|
=> |(9x + 6y – 7)/(3*√13)| = |(3x + 2y + 6)/√13|
=> |(9x + 6y – 7)/3| = |3x + 2y + 6|
=> (9x + 6y – 7)/3 = 3x + 2y + 6 and (9x + 6y – 7)/3 = -(3x + 2y + 6)
=> 9x + 6y – 7 = 3*(3x + 2y + 6) and 9x + 6y – 7 = -3*(3x + 2y + 6)
=> 9x + 6y – 7 = 9x + 6y + 18 and 9x + 6y – 7 = -9x – 6y – 18
Now, 9x + 6y – 7 = 9x + 6y + 18 which is not possible.
Again
9x + 6y – 7 = -9x – 6y – 18
=> 9x + 6y – 7 + 9x + 6y + 18 = 0
=> 18x + 12y + 11 = 0
Hence, the required equation is: 18x + 12y + 11 = 0
Question 22:
A ray of light passing through the point (1, 2) reflects on the x-axis at point A and the reflected ray passes through the point (5, 3).
Find the coordinates of A.
Answer:
Let the incident ray strike x-axis at the point A and the coordinate is (x, 0).

tan θ = (3 – 0)/(5-x)
=> tan θ = = 3/(5 – x) ………….1
Again slope of the incident ray
tan(π – θ) = (0-2)/(x – 1)
=> – tan θ = -2/(x – 1)
=> tan θ = 2/(x – 1) ………2
From equation 1 and 2,
3/(5 – x) = 2/(x – 1)
=> 3(x – 1) = 2(5 – x)
=> 3x – 3 = 10 – 2x
=> 3x + 2x = 10 + 3
=> 5x = 13
=> x = 13/5
Hence, the required point is (13/5, 0)
Question 23:
Prove that the product of the lengths of the perpendiculars drawn from the points
{√(a2 – b2), 0} and {-√(a2 – b2), 0} to the line x cos θ/a + y sin θ/b = 1 is b2.
Answer:
The equation of the given line is
x cos θ/a + y sin θ/b = 1
=> bx cos θ + ay sin θ – ab = 0 …………….1
Length of the perpendicular from the point {√(a2 – b2), 0} to the line 1 is
p1 = |b cos θ * √(a2 – b2) + a sin θ * 0 – ab|/√(b2 cos2 θ + a2 sin2 θ)
= |b cos θ * √(a2 – b2) – ab|/√(b2 cos2 θ + a2 sin2 θ) …….2
Length of the perpendicular from the point {-√(a2 – b2), 0} to the line 1 is
p2 = |b cos θ * {-√(a2 + b2)} + a sin θ * 0 – ab|/√(b2 cos2 θ + a2 sin2 θ)
= |b cos θ * √(a2 + b2) + ab|/√(b2 cos2 θ + a2 sin2 θ) ……….3
Multiply equation 2 and 3, we get
p1p2 = {|b cos θ * √(a2 – b2) – ab|* |b cos θ * √(a2 + b2) + ab|}/{√(b2 cos2 θ + a2 sin2 θ)}2
= {|b cos θ * √(a2 – b2) – ab|* |b cos θ * √(a2 + b2) + ab|}/(b2 cos2 θ + a2 sin2 θ)
= {|b cos θ * √(a2 – b2)} 2 – (ab)2|/(b2 cos2 θ + a2 sin2 θ)
= |b2 cos2 θ * (a2 – b2) – a2 b2|/(b2 cos2 θ + a2 sin2 θ)
= |a2 b2 cos2 θ – b4 cos2 θ – a2 b2|/(b2 cos2 θ + a2 sin2 θ)
= b2|a2 cos2 θ – b2 cos2 θ – a2|/(b2 cos2 θ + a2 sin2 θ)
= b2|a2 cos2 θ – b2 cos2 θ – a2 sin2 θ – a2 cos2 θ|/(b2 cos2 θ + a2 sin2 θ)
= b2|-(b2 cos2 θ + a2 sin2 θ)|/(b2 cos2 θ + a2 sin2 θ)
= b2(b2 cos2 θ + a2 sin2 θ)/(b2 cos2 θ + a2 sin2 θ)
= b2
Hence, p1p2 = b2
Question 24:
A person standing at the junction (crossing) of two straight paths represented by the equations 2x – 3y + 4 = 0 and 3x + 4y – 5 = 0 wants to reach the path whose equation is 6x – 7y + 8 = 0 in the least time. Find equation of the path that he should follow.
Answer:
Given equations are:
2x – 3y + 4 = 0 ………….1
3x + 4y – 5 = 0…………..2
After solving it, we get
x = -1/17, y = 22/17
Suppose that person is standing at point P(-1/17, 22/17)
Again given line is 6x – 7y + 8 = 0
Slope = 6/7
Slope of perpendicular line is = -7/6
Now equation of line passing through (-1/17, 22/17) and perpendicular to 6x – 7y + 8 = 0 is
y – 22/17 = (-7/6)*(x + 1/17)
=> 6(17y – 22)/17 = (-7)*(17x + 1)/17
=> 6(17y – 22) = (-7)*(17x + 1)
=> 102y – 132 = -119x – 7
=> 119x + 102y – 132 + 7 = 0
=> 119x + 102y – 125 = 0
This is the required equation of line.
Bottom Block 3
Click here to visit Official CBSE website
Click here for NCERT solutions
Click here to visit Official Website of NCERT
Click here to download NCERT Textbooks

