Class 9 - Mathematics
Lines And Angles - Exercise 6.1

Top Block 1
Question :1 : In the figure lines AB and CD intersect at O. If∠ AOC + ∠ BOE = 700 and ∠ BOD = 400,find ∠ BOE and reflex ∠ COE.
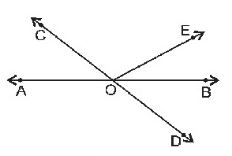
Answer :
Lines AB and CD intersect at O.

Mddle block 1
∠AOC + ∠BOE = 700 (Given) ………………1
∠BOD = 400 (Given) ………………2
Since, ∠AOC = ∠BOD (Vertically opposite angles)
Therefore, ∠AOC = 400 [From equation 2]
and 400 + ∠BOE = 700 [From equation 1]
⇒ ∠BOE = 700– 400 = 300
Also, ∠AOC + ∠BOE + ∠COE = 1800 [Since AOB is a straight line]
⇒ 700 + ∠COE = 1800 [Form equation 1]
⇒ ∠COE = 1800– 700 = 1100
Now, reflex ∠COE = 3600– 1100 = 2500
Hence, ∠BOE = 300 and reflex ∠COE = 2500
Question : 2: In the figure, lines XY and MN intersect at O. If ∠POY = 900 and a : b = 2 : 3, find c.
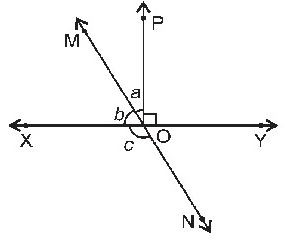
Answer :
In the figure, lines XY and MN intersect at O and ∠ POY = 900.
Also, given a : b = 2 : 3
Let a = 2x and b = 3x.
Since, ∠XOM + ∠POM + ∠POY = 1800 [Linear pair axiom]
⇒ 3x + 2x + 900 = 1800
⇒ 5x = 1800 – 900
⇒ x = 900/50 = 180
So, ∠XOM = b = 3x = 3 * 180 = 540
and ∠POM = a = 2x = 2 * 180 = 360
Now, ∠XON = c = ∠MOY = ∠POM + ∠POY [Vertically opposite angles]
⇒ c = 360 + 900 = 1260
Hence, c = 1260

Question : 3: In the figure, ∠PQR = ∠PRQ, then prove that ∠PQS = ∠ PRT.
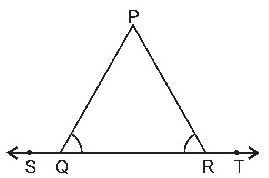
Answer :
∠PQS + ∠PQR = 180°……………1 (Linear pair axiom)
∠PRQ + ∠PRT = 180°……………2 (Linear pair axiom)
But, ∠PQR = ∠PRQ (Given)
From equation 1 and 2, we get
∠PQS = ∠PRT

Question : 4: In the figure, if x + y = w + z, then prove that AOB is a line.

Answer :

Assume AOB is a line.
Therefore, x + y = 180° …………….1 [Linear pair axiom]
and w + z = 180° …………………..2 [Linear pair axiom]
Now, from equation 1 and 2, we get
x + y = w + z
Question : 5: In the figure, POQ is a line. Ray OR is perpendicular to line PQ.OS is another ray lying between rays OP and OR.
Prove that ∠ROS = (∠QOS –∠ POS)/2
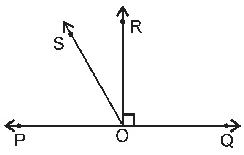
Answer :
From the figure,

∠ROS = ∠ROP –∠POS ……………..1
and ∠ROS = ∠QOS –∠QOR …….2
Adding equation 1 and 2, we get
∠ROS + ∠ROS = ∠QOS –∠QOR + ∠ROP –∠POS
⇒ 2∠ROS = ∠QOS –∠POS [Since ∠QOR = ∠ROP = 900]
⇒ ∠ROS = (∠QOS –∠POS)/2
Question : 6: It is given that ∠ XYZ = 640 and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ ZYP, find ∠ XYQ and reflex ∠QYP.
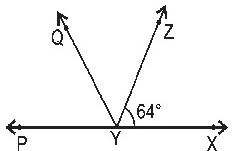
Answer :
From the figure,
∠XYZ = 640 (Given)
Now, ∠ZYP + ∠XYZ = 1800 [Linear pair axiom]
⇒ ∠ZYP + 640 = 1800
⇒ ∠ZYP = 1800 – 640 – 1160
Also, given that ray YQ bisects ∠ZYP.
But, ∠ZYP = ∠QYP = ∠QYZ = 1160
Therefore, ∠QYP = 580 and ∠QYZ = 580
Also, ∠XYQ = ∠XYZ + ∠QYZ
⇒ ∠XYQ = 640 + 580 = 1220
and reflex ∠QYP = 3600–∠QYP = 3600– 580 = 3020 [Since ∠QYP = 580]
Hence, ∠XYQ = 1220 and reflex ∠QYP = 3020

