Class 9 - Mathematics
Areas of Parallelograms and Triangles - Exercise 9.4

Top Block 1
Exercise 9.4
Question :
Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
Answer :
As the parallelogram and the rectangle have the same base and equal area, therefore, these
will also lie between the same parallels.
Consider the parallelogram ABCD and rectangle ABEF as follows.
Here, it can be observed that parallelogram ABCD and rectangle ABEF are between the same parallels AB and CF.
We know that opposite sides of a parallelogram or a rectangle are of equal lengths.
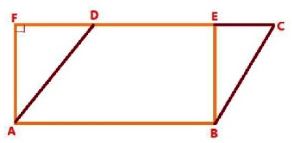
Therefore,
AB = EF [For rectangle]
AB = CD [For parallelogram]
So, CD = EF
⇒ AB + CD = AB + EF … (1)
Of all the line segments that can be drawn to a given line from a point not lying on it, the
perpendicular line segment is the shortest.
So, AF < AD
Similarly, BE < BC
So, AF + BE < AD + BC … (2)
From equations (1) and (2), we obtain
AB + EF + AF + BE < AD + BC + AB + CD
Hence, perimeter of rectangle ABEF < perimeter of parallelogram ABCD
Question : 2: In Fig. 9.30, D and E are two points on BC
such that BD = DE = EC. Show that
ar (ABD) = ar (ADE) = ar (AEC)

Mddle block 1
Can you now answer the question that you have left in the ‘Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?
[Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas.
In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide ∆ABC into n triangles of equal areas.]
Answer :
Let us draw a line segment AM ⊥ BC.
We know that,
Area of a triangle = 1/2 * Base * Altitude
Area(ΔADE) = 1/2 * DE * AM
Area(ΔABD) = 1/2 * BD * AM
Area(ΔAEC) = 1/2 * EC * AM
It is given that DE = BD = EC
So, 1/2 * DE * AM = 1/2 * BD * AM = 1/2 * EC * AM
So, Area (∆ADE) = Area (∆ABD) = Area (∆AEC)
It can be observed that Budhia has divided her field into 3 equal parts.
Question : 3: In Fig. 9.31, ABCD, DCFE and ABFE are parallelograms. Show that: ar(ADE) = ar(BCF)

Answer :
It is given that ABCD is a parallelogram. We know that opposite sides of a parallelogram are
equal.
So, AD = BC ……. (1)
Similarly, for parallelograms DCEF and ABFE, it can be proved that
DE = CF ……………. (2)
and, EA = FB ……. (3)
In ∆ADE and ∆BCF,
AD = BC [Using equation (1)]
DE = CF [Using equation (2)]
EA = FB [Using equation (3)]
So, ∆ADE ≅ BCF [SSS congruence rule]
Hence, Area (∆ADE) = Area (∆BCF)
Question : 4: In Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ.
If AQ intersect DC at P, show that ar(BPC) = ar(DPQ). [Hint: Join AC.]

Answer :
It is given that ABCD is a parallelogram.
AD || BC and AB || DC [Opposite sides of a parallelogram are parallel to each other]
Join point A to point C.
Consider ∆APC and ∆BPC,
∆APC and ∆BPC are lying on the same base PC and between the same parallels PC and AB.
Therefore,
Area (∆APC) = Area (∆BPC) ……….(1)
In quadrilateral ACDQ, it is given that
AD = CQ
Since ABCD is a parallelogram,
AD || BC (Opposite sides of a parallelogram are parallel)
CQ is a line segment which is obtained when line segment BC is produced.
So, AD || CQ
We have,
AC = DQ and AC || DQ
Hence, ACQD is a parallelogram.
Consider ∆DCQ and ∆ACQ
These are on the same base CQ and between the same parallels CQ and AD.
Therefore,
Area (∆DCQ) = Area (∆ACQ)
⇒ Area (∆DCQ) − Area (∆PQC) = Area (∆ACQ) − Area (∆PQC)
⇒ Area (∆DPQ) = Area (∆APC) … (2)
From equations (1) and (2), we obtain
Area (∆BPC) = Area (∆DPQ)
Question : 5: In Fig.9.33, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:
(i) ar(BDE) =ar (ABC)/4
(ii) ar(BDE) = ar(BAE)/2
(iii) ar(ABC) = 2 ar(BEC)
(iv) ar(BFE) = ar(AFD)
(v) ar(BFE) = 2 ar(FED)
(vi) ar (FED) = ar(AFC)/8
[Hint : Join EC and AD. Show that BE || AC and DE || AB, etc.
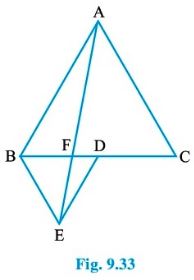
Answer :
(i) Let G and H be the mid-points of side AB and AC respectively.
Line segment GH is joining the mid-points. Therefore, it will be parallel to third side BC and
also its length will be half of the length of BC (mid-point theorem).
GH = BC/2 and GH || BD
GH = BD = DC and GH || BD [D is the mid-point of BC]
Consider quadrilateral GHDB,
GH ||BD and GH = BD
Two line segments joining two parallel line segments of equal length will also be equal and
parallel to each other.
Therefore, BG = DH and BG || DH
Hence, quadrilateral GHDB is a parallelogram.
We know that in a parallelogram, the diagonal bisects it into two triangles of equal area.
Hence, Area (∆BDG) = Area (∆HGD)
Similarly, it can be proved that quadrilaterals DCHG, GDHA, and BEDG are parallelograms and
their respective diagonals are dividing them into two triangles of equal area.
ar(∆GDH) = ar(∆CHD) [For parallelogram DCHG]
ar(∆GDH) = ar(∆HAG) [For parallelogram GDHA]
ar(∆BDE) = ar(∆DBG) [For parallelogram BEDG]
ar(∆ABC) = ar(∆BDG) + ar(∆GDH) + ar(∆DCH) + ar(∆AGH)
ar(∆ABC) = 4 * ar(∆BDE)
Hence, ar(∆BDE) = ar(∆ABC)/4
(ii)Area (∆BDE) = Area (∆AED) [Common base DE and DE||AB]
Area (∆BDE) − Area (∆FED) = Area (∆AED) − Area (∆FED)
Area (∆BEF) = Area (∆AFD) ………….(1)
Area (∆ABD) = Area (∆ABF) + Area (∆AFD)
Area (∆ABD) = Area (∆ABF) + Area (∆BEF) [From equation (1)]
Area (∆ABD) = Area (∆ABE) …………(2)
AD is the median in ∆ABC.
ar(∆ABD) = ar(∆ABC)/2
= 4 * ar(∆BDE)/2 [As proved earlier]
= 2 * ar(∆BDE)
⇒ ar(∆ABD) = 2 * ar(∆BDE) ………..(3)
From equation (2) and (3), we get
2 * ar(∆BDE) = ar(∆ABE)
⇒ ar(∆BDE) = ar(∆ABE)/2
(iii) ar(∆ABE) = ar(∆BEC) [Common base BE and BE||AC]
ar(∆ABF) + ar(∆BEF) = ar(∆BEC)
Using equation (1), we obtain
ar(∆ABF) + ar(∆AFD) = ar(∆BEC)
⇒ ar(∆ABD) = ar(∆BEC)
⇒ ar(∆ABC)/2 = ar(∆BEC)
⇒ ar(∆ABC) = 2 * ar(∆BEC)
(iv) It is seen that ∆BDE and ar ∆AED lie on the same base (DE) and between the parallels DE
and AB.
ar (∆BDE) = ar (∆AED)
ar (∆BDE) − ar (∆FED) = ar (∆AED) − ar (∆FED)
ar (∆BFE) = ar (∆AFD)
(v) Let h be the height of vertex E, corresponding to the side BD in ∆BDE.
Let H be the height of vertex A, corresponding to the side BC in ∆ABC.
In (i), it was shown that ar(∆BDE) = ar(∆ABC)/4
⇒ 1/2 * BD * h = (1/2 * BC * H)/4
⇒ BD * h = (2BD * H)/4
⇒ h = H/2
In (iv), it was shown that ar (∆BFE) = ar (∆AFD).
ar (∆BFE) = ar (∆AFD)
= 1/2 * FD * H
= 1/2 * FD * 2h
= 2(1/2 * FD * h)
= 2 * ar (∆FED)
Hence, ar (∆BFE) = 2 * ar (∆FED)
(vi) Area (AFC) = area (AFD) + area (ADC)
[in (iv), ar(∆BFE) = ar(∆AFD), AD is the median of ΔABC]
= ar (∆BFE) + ar (∆ABC)/2
= ar (∆BFE) + 4 * ar (∆BDE)/2
= ar (∆BFE) + 2 * ar (∆BDE) …………..(5)
Now, by (v), ar (∆BFE) = 2 * ar (∆FED) …………..(6)
ar (∆BDE) = ar (∆BFE) + ar (∆FED) = 2 * ar (∆FED) + ar (∆FED) = 3 * ar (∆FED) ………7
From equation (5), (6) and (7), we get
ar (∆AFC) = 2 * ar (∆FED) + 2 * 3 * ar (∆FED)
= 2 * ar (∆FED) + 6 * ar (∆FED)
= 8 * ar (∆FED)
Hence, ar (∆FED) = ar (∆AFC)/8
Question : 6: Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar(APB) * ar(CPD) = ar(APD) * ar(BPC). [Hint: From A and C, draw perpendiculars to BD.]
Answer :
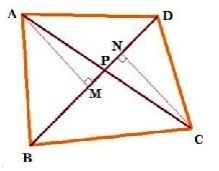
Construction: From A and C, draw perpendiculars AM and CN to BD.
ar (∆APB) * ar (∆CPD) = 1/2 * BP * AM * 1/2 * PD * CN …………..1
ar (∆APD) * ar (∆BPC) = 1/2 * PD * AM * 1/2 * BP * CN …………..2
From equation 1 and 2, we get
ar (∆APB) * ar (∆CPD) = ar (∆APD) * ar (∆BPC)
Question : 7: P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
(i) ar (PRQ) = ar (ARC)/2
(ii) ar (RQC) = 3ar (ABC)/8
(iii) ar (PBQ) = ar (ARC)
Answer :
P and Q are respectively the mid-points of sides AB and BC of ΔABC and R is the mid-point of AP.
Join AQ and PC.

(i) We have,
ar(ΔPQR) = ar(ΔAPQ)/2 [Since QR is a median and ΔAPQ and it divides the triangle into two
other triangles of equal area]
= 1/2 * 1/2 * ar(ΔABQ) [Since QP is a median of ΔABQ]
= 1/4 * ar(ΔABQ)
= 1/4 * 1/2 * ar(ΔABQ) [Since AQ is a median of ΔABQ]
= 1/8 * ar(ΔABQ) ……………..1
Again, ar(ΔARC) = 1/2 * ar(ΔAPC) [Since CR is a median of ΔAPC]
= 1/4 * 1/2 * ar(ΔABQ) [Since CP is a median of ΔABC]
= 1/8 * ar(ΔABQ) ………2
From equation 1 and 2, we get
ar(ΔPQR) = 1/8 * ar(ΔABC)
= 1/2 * 1/2 * ar(ΔABC)
= 1/2 * ar(ΔARC)
(ii) We have,
ar(ΔRQC) = ar(ΔRQA) + ar(ΔAQC) – ar(ΔARC) …………..3
Now, ar(ΔRQA) = 1/2 * ar(ΔPQA) [Since RQ is a median of ΔPQA]
= 1/2 * 1/2 * ar(ΔAQB) [Since PQ is a median of ΔAQB]
= 1/4 * ar(ΔAQB)
= 1/4 * 1/2 * ar(ΔABC) [Since AQ is a median of ΔABC]
= 1/8 * ar(ΔABC) ………..4
ar(ΔAQC) = 1/2 * ar(ΔABC) ……5 [Since AQ is a median of ΔABC]
ar(ΔARC) = 1/2 * ar(ΔAPC) [Since CR is a median of ΔAPC]
= 1/2 * 1/2 * ar(ΔABC) [Since CP is a median of ΔABC]
= 1/4 * ar(ΔABC) ………6
From equation 3, 4, 5 and 6, we get
ar(ΔRQC) = 1/8 * ar(ΔABC) + 1/2 * ar(ΔABC) – 1/4 * ar(ΔABC)
= 3/8 * ar(ΔABC)
(iii) We have,
ar(ΔPBQ) = 1/2 * ar(ΔABQ) [Since PQ is a median of ΔABQ]
= 1/2 * 1/2 * ar(ΔABC) [Since AQ is a median of ΔABC]
= 1/4 * ar(ΔABC)
= ar(ΔARC) [From equation 6]
Question : 8: In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively.
Line segment AX ⊥ DE meets BC at Y. Show that:

(i) ∆ MBC ≅∆ ABD (ii) ar(BYXD) = 2 ar(MBC)
(iii) ar(BYXD) = ar(ABMN) (iv) ∆ FCB ≅∆ ACE
(v) ar(CYXE) = 2 ar(FCB) (vi) ar(CYXE) = ar(ACFG)
(vii) ar(BCED) = ar(ABMN) + ar(ACFG)
Note: Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X.
Answer :
(i) In ΔMBC and ΔABD, we have
BC = BD [Sides of the square BCED]
MB = AB [Sides of the square ABMN]
∠MBC = ∠ABD [since each 900 + ∠ABC]
Therefore, BY SAS criterion of congruence, we have
∆ MBC ≅∆ ABD
(ii) ΔABD and square BYXD have the same base BD and are between the same parallels BD and
AX.
Therefore, ΔABD = 1/2 * ar(BYXD)
But ∆ MBC ≅∆ ABD [Proved in part (i)]
So, ar(∆ MBC) ≅ ar(∆ ABD)
Therefore, ar(∆ MBC) ≅ ar(∆ ABD) = 1/2 * ar(BYXD)
⇒ ar(BYXD) = 2 * ar(∆ MBC)
(iii) Square ABMN and ∆ MBC have the same base MB and are between the same parallels MB
and NAC.
ar(∆ MBC) = 1/2 * ar(ABMN)
⇒ ar(ABMN) = 2 * ar(∆ MBC) = ar(BYXD) [Using part (ii)]
(iv) In ΔACE and ΔBCF, we have
CE = BC [Sides of the square BCED]
AC = CF [Sides of the square ACFG]
∠ACE = ∠BCF [since each 900 + ∠BCA]
Therefore, BY SAS criterion of congruence, we have
∆ ACE ≅ ∆ BCF
(v) ΔACE and square CYXE have the same base CE and are between same parallels CF and AYX.
Therefore, ar(∆ ACE) = 1/2 * ar(CYXE)
⇒ ar(∆ FCB) = 1/2 * ar(CYXE) [Since ∆ ACE ≅∆ BCF in part (iv)]
⇒ ar(CYXE) = 2 * ar(∆ FCB)
(vi) Square ACFG and ∆ BCF have the same base CF and are between the same parallels CF
and BAG.
ar(∆ BCF) = 1/2 * ar(ACFG)
⇒ 1/2 *ar(CYXE) = 1/2 * ar(ACFG) [Using part (v)]
⇒ ar(CYXE) = ar(ACFG)
(vii) From part (iii) and (iv), we have
ar(BYXD) = ar(ABMN)
and ar(CYXE) = ar(ACFG)
On adding, we get
ar(BYXD) + ar(CYXE) = ar(ABMN) + ar(ACFG)
⇒ ar(BCED) = ar(ABMN) + ar(ACFG)

