Class 9 - Mathematics
Surface Areas and Volumes - Exercise 13.4

Top Block 1
Exercise 13.4
Question : 1 : Find the surface area of a sphere of radius:
(i) 10.5 cm (ii) 5.6 cm (iii) 14 cm
Answer :
(i) r = 10.5 cm
Surface area of the sphere = 4πr2
= 4 * (22/7) * (10.5)2
= 4 * (22/7) * 10.5 * 10.5
= 4 * 22 * 10.5 * 1.5
= 1386 cm2
(ii) r = 5.6 cm
Surface area of the sphere = 4πr2
= 4 * (22/7) * (5.6)2
= 4 * (22/7) * 5.6 * 5.6
= 4 * 22 * 5.6 * 0.8
= 394.24 cm2
(iii) r = 14 cm
Surface area of the sphere = 4πr2
= 4 * (22/7) * (14)2
= 4 * (22/7) * 14 * 14
= 4 * 22 * 14 * 2
= 2464 cm2
Question : 2: Find the surface area of sphere of a diameter:
(i) 14 cm (ii) 21 cm (iii) 3.5 m
Answer :
(i) r = 14/2 cm = 7 cm
Surface area of the sphere = 4πr2
= 4 * (22/7) * 72
= 4 * (22/7) * 7 * 7
= 4 * 22 * 7
= 616 cm2
(ii) r = 21/2 = 10.5 cm
Surface area of the sphere = 4πr2
= 4 * (22/7) * (10.5)2
= 4 * (22/7) * 10.5 * 10.5
= 4 * 22 * 10.5 * 1.5
= 1386 cm2
(iii) r = 3.5/2 = 1.75 m
Surface area of the sphere = 4πr2
= 4 * (22/7) * (1.75)2
= 4 * (22/7) * 1.75 * 1.75
= 4 * 22 * 1.75 * 0.25
= 38.5 cm2
Question : 3: Find the total surface area of a hemisphere of radius 10 cm. (Use π = 3.14)
Answer :
Given, radius r = 10 cm
Total surface area of the hemisphere = 3πr2
= 3 * 3.14 * (10)2
= 3 * 3.14 * 100
= 942 cm2
Question : 4: The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
Answer :
When r = 7 cm:
Surface area of the balloon = 4πr2
= 4 * π * 7 * 7 cm2
When R = 14 cm:
Surface area of the balloon = 4πr2
= 4 * π * 14 * 14 cm2
Required ratio of the surface areas of the balloon = (4 * π * 7 * 7)/( 4 * π * 14 * 14)
= 1/4
= 1 : 4
Mddle block 1
Question : 5: A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of Rs 16 per 100 cm2.
Answer :
Here r = 10.5/2 = 5.25 cm
Inner surface area of the bowl = 2πr2
= 2 * (22/7) * (5.25)2
= 2 * (22/7) * 5.25 * 5.25
= 44 * 0.75 * 5.25
= 173.25 cm2
Cost of tin plating 100 cm2 = Rs 16
Cost of tin plating 173.25 cm2 = Rs (16/100) * 173.25
= Rs 0.16 * 173.25
= Rs 27.72
Question : 6: Find the radius of a sphere whose surface area is 154 cm2.
Answer :
Surface area of the sphere = 4πr2
⇒ 154 = 4 * (22/7) * r2
⇒ r2 = (154 * 7)/(4 * 22)
⇒ r2 = (7 * 7)/4
⇒ r2 = 49/4
⇒ r = √(49/4) ⇒ r = 7/2 ⇒ r = 3.5
Hence, radius of the sphere = 3.5 cm.
Question : 7: The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface areas.
Answer :
Let diameter of the earth = 2r
Then radius of the earth = r
So, Diameter of the moon = 2r/4 = r/2
Radius of the moon = (r/2)/2 = r/4
Now, surface area of the moon = 4π(r/4)2
= πr2/4 ……………..1
Surface area of the earth = 4πr2 ……….2
So, Required ratio = (πr2/4)/( 4πr2)
= 1/16
= 1 : 16
Question : 8: A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
Answer :
Inner radius of the bowl (r) = 5 cm
Thickness of the steel = 0.25 cm
So, Outer radius of the bowl (R) = 5 + 0.25 = 5.25 cm
Outer curved surface area of the bowl = 2πR2
= 2 * (22/7) * (5.25)2
= 2 * (22/7) * 5.25 * 5.25
= 2 * 22 * 5.25 * 0.75
= 173.25 cm2
Question : 9: A right circular cylinder just encloses a sphere of radius r (see figure). Find
(i) surface area of the sphere,
(ii) curved surface area of the cylinder,
(iii) ratio of the areas obtained in (i) and (ii).
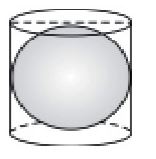
Answer :
Here, radius of the sphere = r
Radius of the cylinder = r
And, height of the cylinder = 2r
(i) Surface area of the sphere = 4πr2
(ii) Curved surface area of the cylinder = 2πrh
= 2π * r * 2r
= 4πr2
(iii) Required ratio = (4πr2)/( 4πr2) = 1/1 = 1 : 1

