Class 10 - Mathematics
Coordinate Geometry - Exercise 7.3

Top Block 1
Exercise 7.3
Question : 1:Find the area of the triangle whose vertices are: (i) (2, 3), (–1, 0), (2, – 4) (ii) (–5, –1), (3, –5), (5, 2)
Answer :
(i) Vertices of triangle are: A(2, 3), B(–1, 0) and C(2, – 4)
Using the formula for area of triangle = (1/2)[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
Now, area of triangle ABC = (1/2)[2(0 + 4) + (-1)(-4 – 3) + 2(3 – 0)]
= (1/2)[8 + 7 + 6]
= 21/2
= 10.5 square units
(ii) Vertices of triangle are: A(–5, –1), B(3, –5), C(5, 2)
Using the formula for area of triangle = (1/2)[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
Now, area of triangle ABC = (1/2)[(-5)(-5 – 2) +3(2 + 1) + 5(-1 + 5)]
= (1/2)[35 + 9 + 20]
= 64/2
= 32 square units
Question : 2:In each of the following find the value of ‘k’, for which the points are collinear.
(i) (7, –2), (5, 1), (3, k) (ii) (8, 1), (k, – 4), (2, –5)
Answer :
(i) A(7, –2), B(5, 1), C(3, k)
Area of triangle formed by three collinear points is zero.
Therefore, the area of triangle ABC = 0
⇒ (1/2)[7(1 – k) + 5(k + 2) + 3(-2 – 1)] = 0
⇒ 7 – 7k + 5k + 10 – 9 = 0
⇒ -2k = -8
⇒ k = 4
(ii) A(8, 1), B(k, – 4), C(2, –5)
Area of triangle formed by three collinear points is zero.
Therefore, the area of triangle ABC = 0
⇒ (1/2)[8(-4 + 5) + k(-5 – 1) + 2(1 + 4)] = 0
⇒ 8 – 6k + 10 = 0
⇒ -6k = -18
⇒ k = 3
Question : 3:Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3).
Find the ratio of this area to the area of the given triangle.
Answer :
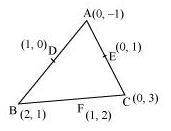
Let D, E and F be the mid-points of the sides of the triangle.
Now, coordinates of d, E and F are given as:
D = {(0 + 2)/2, (-1 + 1)/2} = (1, 0)
D = {(0 + 0)/2, (3 – 1)/2} = (0, 1)
D = {(2 + 0)/2, (1 + 3)/2} = (1, 2)
Now, area of triangle = (1/2)[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
Area of triangle DEF = (1/2)[1(2 – 1) + 1(1 – 0) + 0(0 – 2)]
= (1/2)[1 + 1]
= 1 square units
Area of triangle ABC = (1/2)[0(1 – 3) + 2(3 + 1) + 0(-1 – 1)]
= (1/2)[0 + 8]
= 4 square units
Therefore, required ratio = 1 : 4
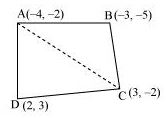
Question : 4:Find the area of the quadrilateral whose vertices, taken in order, are (– 4, – 2), (– 3, – 5), (3, – 2) and (2, 3).
Answer :
Let the vertices of the quadrilateral be A(– 4, – 2), B(– 3, – 5), C(3, – 2) and D(2, 3).
Join AC to form two triangles ABC and ACD.
Mddle block 1
Area of triangle ABC = (1/2)[(-4)(-5 + 2) + (-3)(-2 + 2) + 3(-2 + 5)]
= (1/2)[12 + 0 + 9]
= 21/2 square units
Area of triangle ACD = (1/2)[(-4)(-2 + 3) + 3(3 + 2) + 2(-2 + 2)]
= (1/2)[20 + 15 + 0]
= 35/2 square units
Area of quadrilateral ABCD = Area of ΔABC + Area of ΔACD
= 21/2 + 35/2
= (21 + 35)/2
= 56/2 = 28 square units
Question : 5:You have studied in Class IX, (Chapter 9, Example 3), that a median of a triangle divides it into two triangles of equal areas.
Verify this result for Δ ABC whose vertices are A(4, – 6), B(3, –2) and C(5, 2).
Answer :
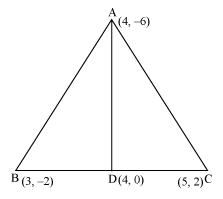
Let D be the mid-point of side BC to Δ ABC.
Therefore, AD is the median in Δ ABC.
Coordinate of point D = {(3 + 5)/2, (-2 + 2)/2} = (4, 0)
Now, area of triangle = (1/2)[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)]
Area of triangle ABD = (1/2)4(-2 – 0) + 3(0 + 6) + 4(-6 + 2)]
= (1/2)[-8 + 18 – 16]
= -6/2
= -3 square units
Since area cannot be negative.
So, area of triangle ABD is 3 square units.
Area of triangle ADC = (1/2)[4(0 – 2) + 4(2 + 6) + 5(-6 – 0)]
= (1/2)[-8 + 32 – 30]
= -6/2
= -3 square units
Since area cannot be negative.
So, area of triangle ABD is 3 square units.
Clearly, median AD has divided triangle ABC in two triangles of equal area.

