Class 10 - Mathematics
Introduction To Trigonometry - Exercise 8.1

Top Block 1
Exercise 8.1
Question : 1:In Δ ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine:
(i) sin A, cos A (ii) sin C, cos C
Answer :
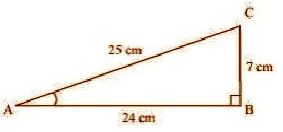
AC2 = AB2 + BC2
⇒ AC2 = 242 + 72
⇒ AC2 = 576 + 49
⇒ AC2 = 625
⇒ AC = √625
⇒ AC = 25
(i) sin A = BC/AC = 7/25, cos A = AB/AC = 24/25
(ii) sin C = AB/AC = 24/25, cos C = BC/AC = 7/25
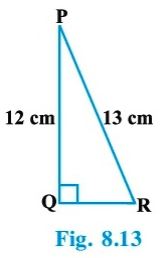
Question : 2:In Fig. 8.13, find tan P – cot R.
Answer :
Mddle block 1
QR2 = PR2 – PQ2
⇒ QR2 = 132 – 122
⇒ QR2 = 169 – 144
⇒ QR2 = 25
⇒ QR = √25
⇒ QR = 5
Hence, tan P – cot R = QR/PQ – QR/PQ
= 5/12 – 5/12
= 0
Question : 3:If sin A = 3/4, calculate cos A and tan A.
Answer :
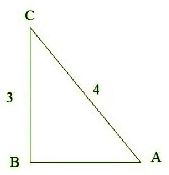
In Δ ABC, by Pythagoras theorem,
AB2 = AC2 – BC2
⇒ AB2 = 42 – 32
⇒ AB2 = 16 – 9
⇒ AB2 = 7
⇒ AB = √7
Hence, cos A = AB/AC = √7/4, tan A = BC/AB = 3/√7
Question : 4:Given 15 cot A = 8, find sin A and sec A.
Answer :
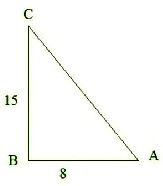
⇒ cot A = 8/15
In Δ ABC, by Pythagoras theorem,
AC2 = AB2 + BC2
⇒ AC2 = 82 + 152
⇒ AC2 = 64 + 225
⇒ AC2 = 289
⇒ AC = √289
⇒ AC = 17
Hence, sin A = BC/AC = 15/17, sec A = AC/AB = 17/8
Question : 5:Given sec θ = 13/12, calculate all other trigonometric ratios.
Answer :
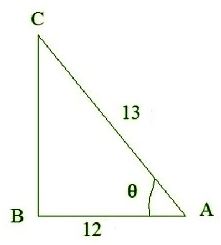
In Δ ABC, by Pythagoras theorem,
BC2 = AC2 – AB2
⇒ BC2 = 132 – 122
⇒ BC2 = 169 – 144
⇒ BC2 = 25
⇒ BC = √25
⇒ BC = 5
Hence, sin θ = BC/AC = 5/13, cos θ = AB/AC = 12/13, tan θ = BC/AB = 5/12
cosec θ = AC/BC = 13/5, cot θ = AB/BC = 12/5
Question : 6:If ∠ A and ∠ B are acute angles such that cos A = cos B, then show that ∠ A = ∠ B
Answer :
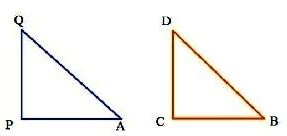
⇒ AP/AQ = BC/BD
⇒ AP/BC = AQ/BD
Let AP/BC = AQ/BD = k ………1
So, AP = k * BC and AQ = k * BD
Now in ΔAPQ and ΔBCD,
PQ/CD = √(AQ2 – AP2)/ √(BD2 – BC2)
= √{(K * BD)2 – (k * BC)2}/ √(BD2 – BC2)
= K√(BD)2 – BC)2/ √(BD2 – BC2)
= K
⇒ PQ/CD = K ………….2
From equation 1 and 2, we get
AP/BC = AQ/BD = PQ/CD
So, ΔAPQ ~ ΔBCD [SSS similarity criteria]
Hence, ∠ A = ∠ B
Question : 7:If cot θ = 7/8, evaluate:
(i) {(1 + sin θ)(1 – sin θ)}/ {(1 + cos θ)(1 – cos θ)} (ii) cot2 θ
Answer :
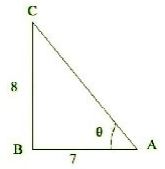
In Δ ABC, by Pythagoras theorem,
AC2 = AB2 + BC2
⇒ AC2 = 82 + 72
⇒ AC2 = 64 + 49
⇒ AC2 = 113
⇒ AC = √113
(i) {(1 + sin θ)(1 – sin θ)}/ {(1 + cos θ)(1 – cos θ)}
= (1 – sin2 θ)/(1 – cos2 θ) [a2 – b2 = (a + b)(a – b)]
= {1 – (7/√113)2}/{1 – (8/√113)2}
= (1 – 49/113)/(1 – 64/113)
= {(113 – 49)/113}/{(113 – 64)/113}
= 64/49
(ii) cot2 θ = (cot θ)2
= (7/8)2
= 49/64
Question : 8:If 3 cot A = 4, check whether (1 – tan2 A)/(1 + tan2 A) = cos2 A – sin2 A or not.
Answer :
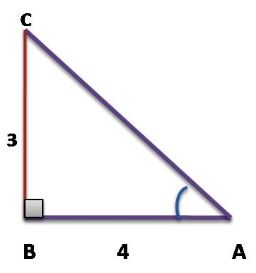
⇒ cot A = 4/3
In Δ ABC, by Pythagoras theorem,
AC2 = AB2 + BC2
⇒ AC2 = 32 + 42
⇒ AC2 = 9 + 16
⇒ AC2 = 25
⇒ AC = √25
⇒ AC = 5
Now, (1 – tan2 A)/(1 + tan2 A) = {1 – (3/4)2}/{1 + (3/4)2}
= {1 – 9/16}/{1 + 9/16}
= {(16 – 9)/16}/{(16 + 9)/16}
= 7/25
And cos2 A – sin2 A = (4/5)2 – (3/5)2
= 16/25 – 9/15
= 7/25
Hence, (1 – tan2 A)/(1 + tan2 A) = cos2 A – sin2 A
Question : 9:In triangle ABC, right-angled at B, if tan A = 1/√3, find the value of:
(i) sin A cos C + cos A sin C (ii) cos A cos C – sin A sin C
Answer :
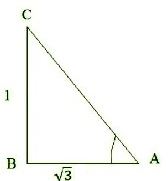
In Δ ABC, by Pythagoras theorem,
AC2 = AB2 + BC2
⇒ AC2 = (√3)2 + 12
⇒ AC2 = 3 + 1
⇒ AC2 = 4
⇒ AC = √4
⇒ AC = 2
(i) sin A cos C + cos A sin C = (1/2) * (1/2) + (√3/2) * (√3/2)
= 1/4 + 3/4
= 4/4
= 1
(ii) cos A cos C – sin A sin C = (√3/2) * (1/2) – (1/2) * (√3/2)
= (√3/4) – (√3/4)
= 0
Question : 10:In Δ PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Answer :
Given, in Δ PQR, angle Q is right-angled.
Let QR = x, therefore, PR = 25 – x
In Δ PQR, by Pythagoras theorem,
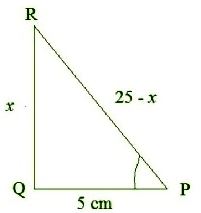
⇒ (25 – x)2 = 52 + x2
⇒ 625 + x2 – 50x = 25 + x2
⇒ 625 – 50x = 25
⇒ 50x = 625 – 25
⇒ 50x = 600
⇒ x = 600/50
⇒ x = 12
Therefore, PR = 25 – 12 = 13
Now, sin P = QR/PR = 12/13, cos P = PQ/PR = 5/13 and tan P = QR/PQ = 12/5
Question : 11:State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1.
(ii) sec A = 12/5 for some value of angle A.
(iii) cos A is the abbreviation used for the cosecant of angle A.
(iv) cot A is the product of cot and A.
(v) sin θ = 4/3 for some angle θ.
Answer :
(i) False.
Because, tan A = Opposite side of angle A/adjacent side of angle A
If opposite side > adjacent side, then the value of tan A is greater than 1.
(ii) True.
Because, tan A = hypotenuse/adjacent side of angle A
And we know that hypotenuse is always greater than adjacent side.
(iii) False.
Because, cos A is used for cosine of angle A.
(iv) False.
Because, cos A is used for cotangent of angle A.
(v) False.
Because, sin θ = opposite side of angle θ/hypotenuse
And we know that hypotenuse is always greater than opposite side.

