Class 9 - Mathematics
Lines And Angles - Exercise 6.2

Top Block 1
Exercise 6.2
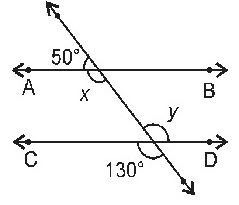
Question : 1: In the figure, find the values of x and y and then show that AB || CD.

Answer :
In the given figure, a transversal intersects two lines AB and CD such that
Mddle block 1
x + 500 = 1800 [Linear pair axiom]
⇒ x = 1800 – 500 = 1300
and y = 1300 [Vertically opposite angles]
Therefore, ∠x = ∠y = 1300 [Alternate angles]
Hence, AB || CD [Converse of alternate angles axiom]
Question : 2: In the figure, if AB || CD, CD || EF and y : z = 3 : 7, find x.

Answer :
In the given figure, AB || CD, CD || EF and y : z = 3 : 7.

Let y = 3a and z = 7a
∠DHI = y [vertically opposite angles]
∠DHI + ∠FIH = 1800 [Interior angles on the same side of the transversal]
⇒ y + z = 1800
⇒ 3a + 7a = 1800
⇒ 10a = 1800
⇒ a = 180
So, y = 3 * 18° = 540
and z = 180 * 7 = 1260
Also, x + y = 1800
⇒ x + 540 = 1800
⇒ x = 1800 – 540 = 1260
Hence, x = 1260
Question : 3: In the figure, if AB || CD, EF ⊥ CD and ∠GED = 126°. Find ∠ AGE, ∠GEF and ∠FGE.

Answer :
In the given figure, AB || CD, EF ⊥ CD and ∠GED = 1260
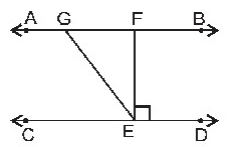
∠AGE = ∠LGE [Alternate angle]
So, ∠AGE = 1260
Now, ∠GEF = ∠GED –∠DEF
= 1260 – 900 = 360 [Since ∠DEF = 900]
Also, ∠AGE + ∠FGE = 1800 [Linear pair axiom]
⇒ 1260 + FGE = 1800
⇒ ∠FGE = 1800– 1260 = 540
Question : 4: In the figure, if PQ || ST, ∠PQR = 1100 and ∠ RST = 1300, find ∠QRS.
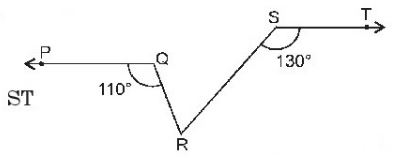
Answer :
Extend PQ to Y and draw LM || ST through R.
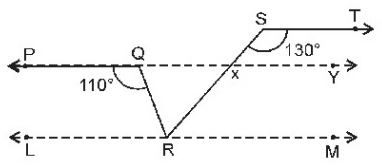
∠TSX = ∠QXS [Alternate angles]
⇒ ∠QXS = 1300
∠QXS + ∠RXQ = 1800 [Linear pair axiom]
⇒ ∠RXQ = 1800– 1300 = 500 …………..1
∠PQR = ∠QRM [Alternate angles]
⇒ ∠QRM = 1100 ………………2
∠RXQ = ∠XRM [Alternate angles]
⇒ ∠XRM = 500 [from equation 1]
∠QRS = ∠QRM –∠XRM
= 1100 – 500 = 600
Question : 5: In the figure, if AB || CD, ∠APQ = 500 and ∠PRD = 127°, find x and y.
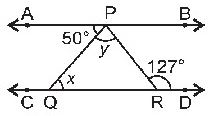
Answer :
In the given figure, AB || CD, ∠APQ = 500 and ∠PRD = 1270
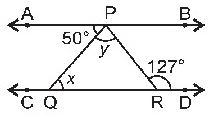
∠APQ + ∠PQC = 1800 [Pair of consecutive interior angles are supplementary]
⇒ 500 + ∠PQC = 1800
⇒ ∠PQC = 1800– 500 = 1300
Now, ∠PQC + ∠PQR = 1800 [Linear pair axiom]
⇒ 1300 + x = 1800
⇒ x = 1800 – 1300 = 500
Also, x + y = 1270 [Exterior angle of a triangle is equal to the sum of the two interior opposite
angles]
⇒ 500 + y = 1270
⇒ y = 1270 – 500 = 770
Hence, x = 500 and y = 770
Question : 6: In the figure, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along
the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.
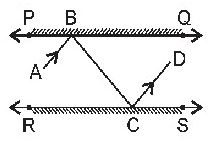
Answer :
At point B, draw BE ⊥ PQ and at point C, draw CF ⊥ RS.
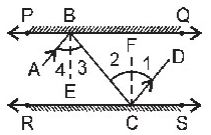
∠1 = ∠2 …………..1 [Angle of incidence is equal to angle of reflection]
∠3 = ∠4 …………..2 [Angle of incidence is equal to angle of reflection]
Also, ∠2 = ∠3 ……3 [Alternate angles]
⇒ ∠1 = ∠4 [From equation 1, 2, and 3]
⇒ 2∠1 = 2∠4
⇒ ∠1 + ∠1 = ∠4 + ∠4
⇒ ∠1 + ∠2 = ∠3 + ∠4 [From (i) and (ii)]
⇒ ∠BCD = ∠ABC
Hence, AB || CD. [Alternate angles are equal]
Hence, Proved.

