Class 10 - Mathematics
Coordinate Geometry - Exercise 7.1

Top Block 1
Exercise 7.1
Question : 1:Find the distance between the following pairs of points:
(i) (2, 3), (4, 1) (ii) (– 5, 7), (– 1, 3) (iii) (a, b), (– a, – b)
Answer :
(i) Distance between two points (x1, y1) and (x2, y2) is given as:
√{(x2 – x1)2 + (y2 – y1)2}
Therefore, the distance between two points (2, 3) and (4, 1) is
D = √{(4 – 2)2 + (1 – 3)2}
⇒ D = √{22 + (-2)2}
⇒ D = √{4 + 4}
⇒ D = √8
⇒ D = 2√2
(ii) Distance between two points (x1, y1) and (x2, y2) is given as:
√{(x2 – x1)2 + (y2 – y1)2}
Therefore, the distance between two points (2, 3) and (4, 1) is
D = √{(-1 + 5)2 + (3 – 7)2}
⇒ D = √{42 + (-4)2}
⇒ D = √{16 + 16}
⇒ D = √32
⇒ D = 4√2
(iii) Distance between two points (x1, y1) and (x2, y2) is given as:
√{(x2 – x1)2 + (y2 – y1)2}
Therefore, the distance between two points (2, 3) and (4, 1) is
D = √{(-a – a)2 + (-b – b)2}
⇒ D = √{(-2a)2 + (-2b)2}
⇒ D = √{4a2 + 4b2}
⇒ D = 2√(a2 + b2)
Question : 2:Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B discussed in Section 7.2.
Answer :
The distance between the points (0, 0) and (36, 15) = √{(36 – 0)2 + (15 – 0)2}
= √(362 + 152)
= √(1296 + 225)
= √1521
= 39
Yes, we can find the distance between the given towns A and B.
Let town A at origin i.e. point (0, 0)
Therefore, town B will be at point (36, 15) with respect to town A.
Hence, the distance between the given town A and B will be 39 km.
Question : 3:Determine if the points (1, 5), (2, 3) and (– 2, – 11) are collinear.
Answer :
Let the points (1, 5), (2, 3), and (−2, −11) be representing the vertices A, B, and C of the given
triangle respectively.
Let A = (1, 5), B = (2, 3) and C = (-2, -11)
Now, AB = √{(1 – 2)2 + (5 – 3)2} = √{(-1)2 + 22} = √(1 + 4) = √5
BC = √{(-2 – 2)2 + (-11 – 3)2} = √{(-4)2 + (-14)2} = √(16 + 196) = √212
CA = √{(-2 – 1)2 + (-11 – 5)2} = √{(-3)2 + (-16)2} = √(9 + 256) = √265
Since AB + BC ≠ CA
Therefore, the points (1, 5), (2, 3), and (−2, −11) are not collinear.
Question : 4:Check whether (5, – 2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.
Answer :
Let the points (5, −2), (6, 4), and (7, −2) are representing the vertices A, B, and C of the given
triangle respectively.
Now, AB = √{(5 – 6)2 + (-2 – 4)2} = √{(-1)2 + (-6)2} = √(1 + 36) = √37
BC = √{(6 – 7)2 + (4 + 2)2} = √{(-1)2 + 62} = √(1 + 36) = √37
CA = √{(5 – 7)2 + (-2 + 2)2} = √{(-2)2 + 0} = √4 = 2
Therefore, AB = BC
Since two sides are equal in length, therefore, ABC is an isosceles triangle.
Question : 5:In a classroom, 4 friends are seated at the points
A, B, C and D as shown in Fig. 7.8. Champa and Chameli walk into the class and after observing for a few minutes
Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees.
Using distance formula, find which of them is correct.
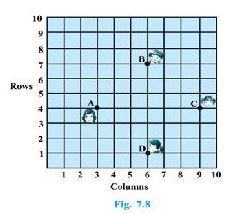
Answer :
It can be observed that A (3, 4), B (6, 7), C (9, 4), and
D (6, 1) are the positions of these 4 friends.
Now, AB = √{(3 – 6)2 + (4 – 7)2} = √{(-3)2 + (-3)2} = √(9 + 9) = √18 = 3√2
BC = √{(6 – 9)2 + (7 – 4)2} = √{(-3)2 + 32} = √(9 + 9) = √18 = 3√2
CD = √{(9 – 6)2 + (4 – 1)2} = √{32 + 32} = √(9 + 9) = √18 = 3√2
AD = √{(3 – 6)2 + (4 – 1)2} = √{(-3)2 + 32} = √(9 + 9) = √18 = 3√2
Diagonal AC = √{(3 – 9)2 + (4 – 4)2} = √{(-6)2 + 0} = 6
Diagonal BD = √{(6 – 6)2 + (7 – 1)2} = √{0 + 62} = 6
It can be observed that all sides of this quadrilateral ABCD are of the same length and also the
diagonals are of the same length.
Therefore, ABCD is a square and hence, Champa is correct.
Question : 6:Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
(i) (– 1, – 2), (1, 0), (– 1, 2), (– 3, 0)
(ii) (–3, 5), (3, 1), (0, 3), (–1, – 4)
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
Answer :
(i) Let the points (−1, −2), (1, 0), (−1, 2), and (−3, 0) be representing the vertices A, B, C, and D
of the given quadrilateral respectively.
Now, AB = √{(-1 – 1)2 + (-2 – 0)2} = √{(-2)2 + (-2)2} = √(4 + 4) = √8 = 2√2
BC = √{(1 + 1)2 + (0 – 2)2} = √{22 + (-2)2} = √(4 + 4) = √8 = 2√2
CD = √{(-1 + 3)2 + (2 – 0)2} = √{22 + 22} = √(4 + 4) = √8 = 2√2
AD = √{(-1 + 3)2 + (-2 – 0)2} = √{22 + (-2)2} = √(4 + 4) = √8 = 2√2
Diagonal AC = √{(-1 + 1)2 + (-2 – 2)2} = √{0 + (-4)2} = √16 = 4
Diagonal BD = √{(1 + 3)2 + (0 – 0)2} = √(42 + 0) = √16 = 4
It can be observed that all sides of this quadrilateral are of the same length and also, the
diagonals are of the same length. Therefore, the given points are the vertices of a square.
(ii) Let the points (− 3, 5), (3, 1), (0, 3), and (−1, −4) be representing the vertices A, B, C, and D
of the given quadrilateral respectively.
Now, AB = √{(-3 – 3)2 + (5 – 1)2} = √{(-6)2 + 42} = √(36 + 16) = √52 = 2√13
BC = √{(3 – 0)2 + (1 – 3)2} = √{32 + (-2)2} = √(9 + 4) = √13
CD = √{(0 + 1)2 + (3 + 4)2} = √{12 + 72} = √(1 + 49) = √50 = 5√2
AD = √{(-3 + 1)2 + (5 + 4)2} = √{(-2)2 + 92} = √(4 + 81) = √85
It can be observed that all sides of this quadrilateral are of different lengths.
Therefore, it can be said that it is only a general quadrilateral, and not specific such as square,
rectangle, etc.
(iii)Let the points (4, 5), (7, 6), (4, 3), and (1, 2) be representing the vertices A, B, C, and D of
the given quadrilateral respectively.
Now, AB = √{(4 – 7)2 + (5 – 6)2} = √{(-3)2 + (-1)2} = √(9 + 1) = √10
BC = √{(7 – 4)2 + (6 – 3)2} = √{32 + 32} = √(9 + 9) = √18
CD = √{(4 – 1)2 + (3 – 2)2} = √{32 + 12} = √(9 + 1) = √10
AD = √{(4 – 1)2 + (5 – 2)2} = √{32 + 32} = √(9 + 9) = √18
Diagonal AC = √{(4 – 4)2 + (5 – 3)2} = √{0 + 22} = √4 = 2
Diagonal BD = √{(7 – 1)2 + (6 – 2)2} = √(62 + 42) = √(36 + 16) = √52 = 13√2
It can be observed that opposite sides of this quadrilateral are of the same length. However,
the diagonals are of different lengths. Therefore, the given points are the vertices of a
parallelogram.
Mddle block 1
Question : 7:Find the point on the x-axis which is equidistant from (2, –5) and (–2, 9).
Answer :
Let the point on x-axis is (x, 0)
Now √{(2 – x )2 + (-5 – 0) 2} = √{(-2 – x)2 + (-9 – 0) 2}
Squaring on both sides, we get
⇒ (2 – x)2 + (-5 – 0)2 = (-2 – x)2 + (-9 – 0)2
⇒ (2 – x)2 + (-5) 2 = (-2 – x)2 + (-9)2
⇒ 4 + x2 – 4x + 25 = 4 + x2 + 4x + 81
⇒ – 4x + 25 = 4x + 81
⇒ 4x + 4x = 25 – 81
⇒ 8x = -56
⇒ x = -56/8
⇒ x = -7
So, the point on x-axis is (-7, 0)
Question : 8:Find the values of y for which the distance between the points P(2, – 3) and Q(10, y) is 10 units.
Answer :
It is given that the distance between (2, −3) and (10, y) is 10.
Therefore, √{(2 – 10)2 + (-3 – y)2} = 10
⇒ √{(-8)2 + (-3 – y)2} = 10
⇒ √{64 + (-3 – y)2} = 10
Squaring on both sides, we get
⇒ 64 + (-3 – y)2 = 100
⇒ (-3 – y)2 = 100 – 64
⇒ (-3 – y)2 = 36
⇒ (3 + y)2 = 36
⇒ 3 + y = ±√36
⇒ 3 + y = ±6
⇒ 3 + y = 6 or 3 + y = -6
⇒ y = 3 or -9
Question : 9:If Q(0, 1) is equidistant from P(5, –3) and R(x, 6), find the values of x. Also find the distances QR and PR.
Answer :
Q(0, 1) is equidistant from P(5, -3) and R(x, 6).
Therefore, QP = QR
⇒ √{(5 – 0)2 + (-3 – 1)2} = √{(x – 0)2 + (6 – 1)2}
⇒ √(25 + 16) = √{x2 + 25}
Squaring on both sides, we get
⇒ 25 + 16 = x2 + 25 ⇒ x2 = 16 ⇒ x = ±4
If x = 4,
QR = √{(4 – 0)2 + (6 – 1)2} = √(16 + 25) = √41
QR = √{(4 – 5)2 + (6 + 3)2} = √(1 + 81) = √82
If x = -4,
QR = √{(-4 – 0)2 + (6 – 1)2} = √(16 + 25) = √41
QR = √{(-4 – 5)2 + (6 + 3)2} = √(81 + 81) = √162 = 9√2
Question : 10:Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (– 3, 4).
Answer :
Point P(x, y) is equidistant from A(3, 6) and B(-3, 4).
Therefore, PA = PB
⇒ √{(3 – x)2 + (6 – y)2} = √{(-3 – x)2 + (4 – y)2}
Squaring on both sides, we get
⇒ (3 – x)2 + (6 – y)2 = (-3 – x)2 + (4 – y)2
⇒ 9 + x2 – 6x + 36 + y2 – 12y = 9 + x2 + 6x + 16 + y2 – 8y
⇒ -12x – 4y = -20
⇒ 3x + y = 5
This is the required relation between x and y.

